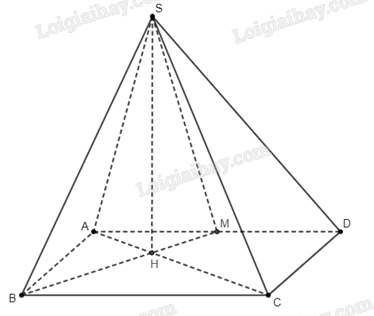
Giải bài 44 trang 104 sách bài tập toán 11 - Cánh diềuCho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(\left( {SAC} \right) \bot \left( {ABCD} \right)\). Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(\left( {SAC} \right) \bot \left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(AD\), \(\left( {SBM} \right) \bot \left( {ABCD} \right)\). Giả sử \(SA = 5a\), \(AB = 3a\), \(AD = 4a\) và góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(\varphi \). Tính \(\cos \varphi \). Phương pháp giải - Xem chi tiết Gọi \(H\) là giao điểm của \(BM\) và \(AC\). Ta chứng minh \(SH \bot \left( {ABCD} \right)\), từ đó suy ra \(\varphi = \widehat {SAH}\). Lời giải chi tiết
Gọi \(H\) là giao điểm của \(BM\) và \(AC\). Dễ dàng chứng minh được \(SH\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBM} \right)\). Hơn nữa, do \(\left( {SAC} \right) \bot \left( {ABCD} \right)\) và \(\left( {SBM} \right) \bot \left( {ABCD} \right)\), ta suy ra \(SH \bot \left( {ABCD} \right)\), tức \(H\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\). Do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) chính là góc \(\widehat {SAH}\), tức là \(\varphi = \widehat {SAH}\). Suy ra \(\cos \varphi = \cos \widehat {SAH} = \frac{{AH}}{{SA}}\). Vì \(ABCD\) là hình chữ nhật, nên \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\). Ta có \(AM = \frac{1}{2}AD = \frac{1}{2}.4a = 2a\). Do \(AM\parallel BC\), ta suy ra \(\frac{{AH}}{{HC}} = \frac{{AM}}{{BC}} = \frac{{2a}}{{4a}} = \frac{1}{2}\). Như vậy \(\frac{{AH}}{{AC}} = \frac{1}{3}\). Suy ra \(AH = \frac{{AC}}{3} = \frac{{5a}}{3}\). Do đó \(\cos \varphi = \frac{{AH}}{{SA}} = \frac{{\frac{{5a}}{3}}}{{5a}} = \frac{1}{3}\).
|