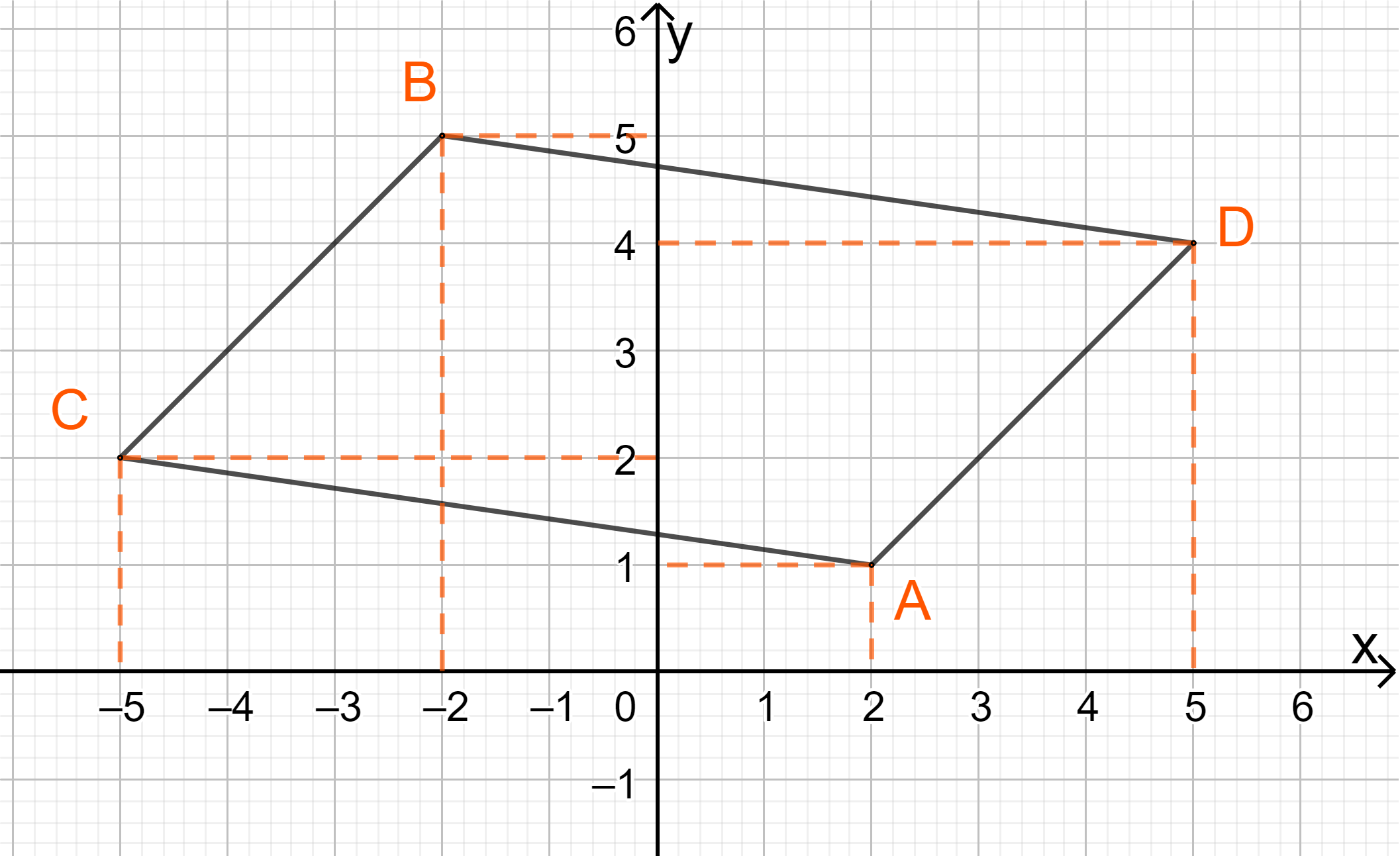
Giải bài 4.35 trang 72 SGK Toán 10 – Kết nối tri thức

Đề bài

Trong mặt phẳng tọa độ Oxy, cho A (2; 1), B (-2; 5) và C (-5; 2).

a) Tìm tọa độ của các vectơ $\overrightarrow {BA}$ và $\overrightarrow {BC}$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Lời giải chi tiết

a) Ta có:  $\overrightarrow {BA}  = (2 - ( - 2);1 - 5) = (4; - 4)$ và $\overrightarrow {BC}  = ( - 5 - ( - 2);2 - 5) = ( - 3; - 3)$

b)

Ta có: $\overrightarrow {BA} .\overrightarrow {BC}  = 4.( - 3) + ( - 4).( - 3) = 0$

$\Rightarrow \overrightarrow {BA}  \bot \overrightarrow {BC}$ hay $\widehat {ABC} = {90^o}$

Vậy tam giác ABC vuông tại B.

Lại có: $AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{4^2} + {{( - 4)}^2}}  = 4\sqrt 2$; $BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{3^2} + {{( - 3)}^2}}  = 3\sqrt 2$

Và $AC = \sqrt {A{B^2} + B{C^2}}  = 5\sqrt 2$ (do $\Delta ABC$vuông tại B).

Diện tích tam giác ABC là: ${S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}.4\sqrt 2 .3\sqrt 2  = 12$

Chu vi tam giác ABC là: $AB + BC + AC = 4\sqrt 2  + 3\sqrt 2  + 5\sqrt 2  = 12\sqrt 2$

c) Tọa độ của trọng tâm G là $\left( {\frac{{2 + ( - 2) + ( - 5)}}{3};\frac{{1 + 5 + 2}}{3}} \right) = \left( {\frac{{ - 5}}{3};\frac{8}{3}} \right)$

d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).

Ta có: $\overrightarrow {CB}  = ( 3; 3)$ và $\overrightarrow {AD}  = (a - 2;b - 1)$

Vì BCAD là một hình bình hành  nên $\overrightarrow {AD}  = \overrightarrow {CB}$

$\begin{array}{l} \Leftrightarrow (a - 2;b - 1) = ( 3;3)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 2 =  3\\b - 1 =  3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  5 \\b = 4\end{array} \right.\end{array}$

Vậy D có tọa độ (5; 4)