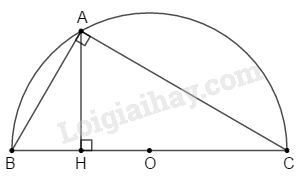
Bài 42 trang 174 SBT toán 9 tập 2

Đề bài

Độ dài các cạnh của một tam giác \(ABC\) vuông tại \(A\), thỏa mãn các hệ thức sau:

\(BC = AB + 2a \)  (1)

\(\displaystyle AC = {1 \over 2}\left( {BC + AB} \right)\) (2)

\(a\) là một độ dài cho trước

a) Tính theo \(a\), độ dài các cạnh và chiều cao \(AH\) của tam giác.

b) Tam giác \(ABC\) nội tiếp được trong nửa hình tròn tâm \(O.\) Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác đó.

c) Cho tam giác \(ABC\) quay một vòng quanh cạnh huyền \(BC.\) Tính tỉ số diện tích giữa các phần do các dây cung \(AB\) và \(AC\) tạo ra.

Lời giải chi tiết

a) Đặt độ dài cạnh \(AB = x\); điều kiện \(x > 0\).

Theo điều kiện (1) ta có: \(BC = x + a\)  (3)

Từ (2) và (3) \( \Rightarrow\displaystyle AC = {1 \over 2}\left( {x + 2a + x} \right) = x + a\)

Áp dụng định lí Pitago vào \(\Delta ABC\) vuông tại A, ta có:

\(B{C^2} = A{B^2} + A{C^2}\)

\( \Rightarrow {\left( {x + 2a} \right)^2} = {x^2} + {\left( {x + a} \right)^2}\)

\( \Rightarrow {x^2} + 4ax + 4{a^2} = {x^2} + {x^2} + 2ax \)\(\,+ {a^2} \)

\( \Rightarrow{x^2} - 2ax - 3{a^2} = 0 \)

\( \Delta = {\left( { - 2a} \right)^2} - 4.1\left( { - 3{a^2}} \right) \)\(\,= 4{a^2} + 12{a^2} = 16{a^2} > 0 \)

\(\Rightarrow \sqrt \Delta = \sqrt {16{a^2}} = 4a \)

\(\displaystyle {x_1} = {{2a + 4a} \over {2.1}} = {{6a} \over 2} = 3a \)

\(\displaystyle {x_2} = {{2a - 4a} \over {2.1}} = - a \)

Vì \(x > 0\) \( \Rightarrow {x_2} =  - a\)  (loại)

Vậy cạnh \(AB = 3a; AC = 3a + a = 4a;\) \(BC = 3a + 2a =5a\).

Ta có \(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông \(ABC)\)

\( \displaystyle \Rightarrow AH = {{AB.AC} \over {BC}} = {{3a.4a} \over {5a}} \)\(\,\displaystyle  = {{12a} \over 5}\)

b) Diện tích của \(\Delta ABC\) là:

\(\displaystyle {S_1} = {1 \over 2}AB.AC = {1 \over 2}.3a.4a = 6{a^2}\) (đơn vị diện tích)

\(\Delta ABC\) nội tiếp trong đường tròn (O) có bán kính: \(\displaystyle R = {{BC} \over 2} = {{5a} \over 2}\)

Diện tích nửa hình tròn là: \(\displaystyle {S_2} = {1 \over 2}\pi .{r^2} = {1 \over 2}\pi .{\left( {{{5a} \over 2}} \right)^2} \)\(\,\displaystyle  = {{25\pi {a^2}} \over 8}\)

Phần diện tích nửa hình tròn nằm ngoài tam giác là:

\(\displaystyle S = {S_2} - {S_1} = {{25\pi {a^2}} \over 8} - 6{a^2}\)\(\,\displaystyle = {{{a^2}} \over 8}\left( {25\pi  - 48} \right)\)

c) Khi quay \(\Delta ABC\) một vòng quanh cạnh \(BC\) thì \(AB\) và \(AC\) vạch lên hai hình nón có bán kính đáy là \(AH.\)

Diện tích xung quanh hình nón do dây cung \(AB\) tạo ra là: 

\(\displaystyle {S_1} = \pi .AH.AB = \pi .AH.3a\)

Diện tích xung quanh hình nón do dây cung cung \(AC\) tạo ra là:

\( {S_2} = \pi .AH.AC = \pi AH.4a \)

Tỉ số diện tích giữa các phần do các dây cung \(AB\) và \(AC\) tạo ra là:

\(\displaystyle {{{S_1}} \over {{S_2}}} = {{\pi .AH.3a} \over {\pi .AH.4a}} = {3 \over 4}  \).

HocTot.Nam.Name.Vn