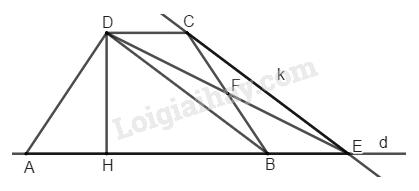
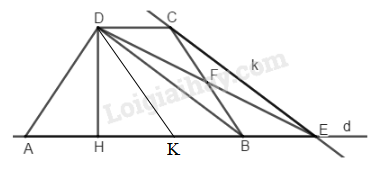
Bài 4.2 phần bài tập bổ sung trang 162 SBT toán 8 tập 1

Đề bài

Cho hình thang \(ABCD\) có đáy nhỏ \(CD\) và đáy lớn \(AB\)

a) Hãy vé tam giác \(ADE\) mà diện tích của nó bằng diện tích hình thang đã cho. Từ đó suy ra cách tính diện tích hình thang dựa vào độ dài hai cạnh đáy và độ dài đường cao của hình thang.

b) Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh \(D\) của nó.

Lời giải chi tiết

a) Từ điểm C kẻ đường thẳng k song song với BD và k cắt đường thẳng AB tại E.

Khi đó ta có \(DC//BE\) và \(BD//CE\) nên \(DCEB\) là hình bình hành

Gọi F là giao điểm của DE và BC, suy ra F là trung điểm của DE và BC (tính chất) 

Hay \(FD=FE,FC=FB\) 

Suy ra \(∆ DFC = ∆ EFB \,(c.g.c)\)

Do đó \({S_{DFC}} = {S_{EFB}}\) (*)

Ta có: 

\(\begin{array}{l}
{S_{ABCD}} = {S_{ADEB}} + {S_{DFC}}\\
{S_{ADE}} = {S_{ADEB}} + {S_{FBE}}
\end{array}\)

Kết hợp với (*) suy ra: \({S_{ABCD}} = {S_{ADE}}\)

Vì \(DCEB\) là hình bình hành \(⇒ DC = BE\)

\(AE = AB + BE = AB + DC\)

\({S_{ADE}} = \dfrac{1}{2}DH.AE \\ =\dfrac{1}{2}DH.\left( {AB + CD} \right)\)

Vậy : \({S_{ABCD}} = \dfrac{1}{2}DH.\left( {AB + CD} \right)\)

b) 

Dựa trên hình vẽ câu a ta chọn điểm \(K\) là trung điểm \(AE.\)

Ta nối \(DK\) cắt hình thang theo đường \(DK\) ta có hai phần diện tích bằng nhau:

Một phần là \(∆ ADK\) có \(AK = \dfrac{AB + CD}{2}\)

Một phần là hình thang \(BCDK\) có hai đáy \(CD + BK = \dfrac{AB + CD}{2}\)

Và có chiều cao bằng nhau nên có diện tích bằng nhau.

HocTot.Nam.Name.Vn