SBT Toán 9 - giải SBT Toán 9 - Cánh diều

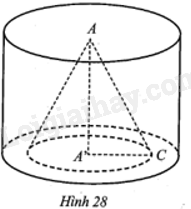
Giải bài 40 trang 137 sách bài tập toán 9 - Cánh diều tập 2

Từ một khối gỗ hình trụ (T) với hai đường tròn đáy là (A; R), (A’; R) và đường cao AA’ = h, người ta khoét đi một khối hình nón (N) có bán kính đường tròn đáy (A'C = frac{2}{3}R) và đường cao trùng với đường cao của hình trụ (T) (Hình 28). Hỏi thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng bao nhiêu phần trăm thể tích của khối gỗ (T) ban đầu (làm tròn kết quả đến hàng phần mười)?

Tổng hợp Đề thi vào 10 có đáp án và lời giải

Toán - Văn - Anh

Đề bài

Từ một khối gỗ hình trụ (T) với hai đường tròn đáy là (A; R), (A’; R) và đường cao AA’ = h, người ta khoét đi một khối hình nón (N) có bán kính đường tròn đáy $A'C = \frac{2}{3}R$ và đường cao trùng với đường cao của hình trụ (T) (Hình 28). Hỏi thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng bao nhiêu phần trăm thể tích của khối gỗ (T) ban đầu (làm tròn kết quả đến hàng phần mười)?

Phương pháp giải - Xem chi tiết

Dựa vào: Thể tích hình trụ: $V = \pi {r^2}h$ .

Thể tích của hình nón: $V = \frac{1}{3}\pi {r^2}h$ .

Lời giải chi tiết

Thể tích của khối gỗ hình trụ (T) là: πR²h.

Thể tích của khối gỗ hình nón (N) là: $\frac{1}{3}\pi .{\left( {\frac{2}{3}R} \right)^2}.h = \frac{4}{{27}}\pi {R^2}h$ .

Thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối gỗ hình nón (N) là

$\pi {R^2}h - \frac{4}{{27}}\pi {R^2}h = \frac{{23}}{{27}}\pi {R^2}h$ .

Tỉ số phần trăm của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) so với thể tích của khối gỗ (T) ban đầu là $\frac{{\frac{{23}}{{27}}\pi {R^2}h}}{{\pi {R^2}h}}.100\% \approx 85,2\%$ .

Vậy thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng khoảng 85,2% thể tích của khối gỗ (T) ban đầu.

Chia sẻ

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Giải bài 41 trang 137 sách bài tập toán 9 - Cánh diều tập 2
Từ một miếng tôn có dạng hình vuông ABCD cạnh 4 dm, người ta cắt ra một phần tư hình tròn tâm A bán kính AB = 4 dm (như phần được tô màu ở Hình 29) và cuộn lại thành một cái phễu hình nón. Tính chiều cao của cái phễu đó (theo đơn vị decimét và làm tròn kết quả đến hàng phần trăm).
Giải bài 42 trang 137 sách bài tập toán 9 - Cánh diều tập 2
Một hình nón có bán kính đáy là 8 cm, đường sinh là 17 cm. Một hình cầu có thể tích bằng thể tích hình nón đó. Tính bán kính hình cầu (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười).
Giải bài 43 trang 137 sách bài tập toán 9 - Cánh diều tập 2
Cần bao nhiêu lít nước để đổ đầy (frac{3}{4}) một bình nuôi cá cảnh? Biết bình nuôi cá cảnh đó có dạng một phần hình cầu và có thể tích bằng (frac{5}{6}) thể tích một hình cầu có đường kính là 30 cm.
Giải bài 44 trang 137 sách bài tập toán 9 - Cánh diều tập 2
Một cốc nước có dạng hình trụ chiều cao 20 cm, bán kính đáy là 4 cm, lượng nước ban đầu trong cốc cao 9 cm. Người ta thả chìm vào cốc nước đó 4 viên bi thuỷ tinh hình cầu có cùng bán kính là 3 cm. Hỏi sau khi thả vào cốc nước 4 viên bi thuỷ tinh trên, mực nước trong cốc cách miệng cốc bao nhiêu centimét?
Giải bài 39 trang 137 sách bài tập toán 9 - Cánh diều tập 2
Bác Long đã chi tiền để làm một cái bể hình trụ có bán kính đường tròn đáy là 0,8 m và có thể tích là 1,12π m3. Đáy bể làm bằng bê tông giá 100 000 đồng/m2. Phần thân làm bằng tôn inox giá 15 000 đồng/m2. Phần nắp làm bằng nhôm giá 12 000 đồng/m2. Hỏi số tiền bác Long đã chi để làm được cái bể đó là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?

Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10