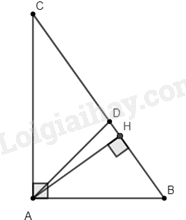
Giải bài 4 trang 57 SGK Toán 8 tập 2– Chân trời sáng tạo

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,AC = 4cm.\) Đường phân giác của góc \(A\) cắt \(BC\) tại \(D\).

a) Tính \(BC,BD,DC\).

b) Vẽ đường cao \(AH\). Tính \(AH,HD\) và \(AD\).

Lời giải chi tiết

a)

Xét tam giác \(ABC\) vuông tại \(A\) ta có:

\(A{B^2} + A{C^2} = B{C^2}\)

\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)

\( \Leftrightarrow B{C^2} = 25\)

\( \Rightarrow BC = 5cm\)

Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)

Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:

\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)

\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)

\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)

Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).

b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:

\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)

Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)

\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).

Xét tam giác \(AHB\) vuông tại \(H\) ta có:

\(A{H^2} + H{B^2} = A{B^2}\)

\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)

\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)

\( \Leftrightarrow H{B^2} = 3,24\)

\( \Rightarrow HB = 1,8cm\)

\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).

Xét tam giác \(AHD\) vuông tại \(H\) ta có:

\(A{H^2} + H{D^2} = A{D^2}\)

\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)

\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)

\( \Rightarrow AD \approx 2,95cm\)

Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).