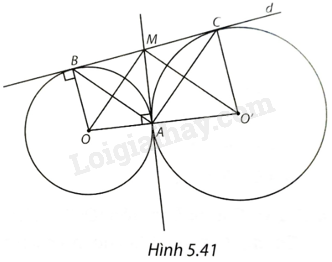
Giải bài 4 trang 121 vở thực hành Toán 9Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó (B in left( O right)) và (C in left( {O'} right)). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng: a) Đường thẳng MA tiếp xúc với (O’); b) Điểm M là trung điểm của đoạn thẳng BC từ đó suy ra ABC là tam giác vuông. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng: a) Đường thẳng MA tiếp xúc với (O’); b) Điểm M là trung điểm của đoạn thẳng BC từ đó suy ra ABC là tam giác vuông. Phương pháp giải - Xem chi tiết a) + Chứng minh \(A \in OO'\). + Chứng minh \(MA \bot AO\) suy ra \(MA \bot AO'\). Do đó, MA là tiếp tuyến của (O’). b) + Chứng minh \(MA = MB\), \(MA = MC\) nên \(MA = MB = MC\). + Do đó, M là trung điểm của BC. + Tam giác ABC có đường trung tuyến AM bằng \(\frac{1}{2}\)BC nên là tam giác vuông tại A. Lời giải chi tiết (H.5.41)
a) Hai đường tròn (O) và (O’) tiếp xúc ngoài tại A nên \(A \in OO'\). Vì MA là tiếp tuyến của (O) tại A nên \(MA \bot AO\) tại A, từ đó suy ra \(MA \bot AO'\). Do đó, MA là tiếp tuyến của (O’). b) MA và MB là hai tiếp tuyến của (O) cắt nhau tai M nên \(MA = MB\). Tương tự đối với đường tròn (O’), ta cũng có \(MA = MC\). Do đó, \(MA = MB = MC\). Do đó, \(MB = MC\). Vậy M là trung điểm của BC. Tam giác ABC có đường trung tuyến AM bằng \(\frac{1}{2}\)BC nên là tam giác vuông tại A.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
