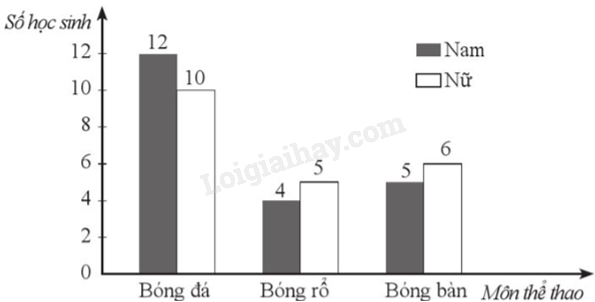
Giải bài 39 trang 39 sách bài tập toán 9 - Cánh diều tập 2Thầy Nam điều tra sở thích chơi thể thao của học sinh lớp 9A do thầy phụ trách (mỗi học sinh chỉ nêu một môn thể thao yêu thích nhất). Biểu đồ cột kép ở Hình 20 biểu diễn số học sinh nam và số học sinh nữ của lớp 9A có sở thích chơi một số môn thể thao: Bóng đá, Bóng rổ, Bóng bàn mà thầy Nam đã điều tra. Chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra. Tính xác suất của mỗi biến cố sau: a) A: “Học sinh được chọn là nam"; b) B: “Học sinh được chọn là nữ và yêu thích môn Bóng đá"; c) Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Thầy Nam điều tra sở thích chơi thể thao của học sinh lớp 9A do thầy phụ trách (mỗi học sinh chỉ nêu một môn thể thao yêu thích nhất). Biểu đồ cột kép ở Hình 20 biểu diễn số học sinh nam và số học sinh nữ của lớp 9A có sở thích chơi một số môn thể thao: Bóng đá, Bóng rổ, Bóng bàn mà thầy Nam đã điều tra. Chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra. Tính xác suất của mỗi biến cố sau: a) A: “Học sinh được chọn là nam"; b) B: “Học sinh được chọn là nữ và yêu thích môn Bóng đá"; c) C: “Học sinh được chọn là nam và yêu thích môn Bóng bàn hoặc Bóng rổ".
Phương pháp giải - Xem chi tiết Bước 1: Tính tổng số kết quả có thể xảy ra khi chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra. Bước 2: Đếm số kết quả thuận lợi cho từng biến cố. Bước 3: Lập tỉ số giữa số liệu ở bước 2 và bước 1. Lời giải chi tiết Các kết quả có thể xảy ra khi chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra là: 12 +10 + 4 + 5 + 5 + 6 = 42 kết quả. a) Các kết quả thuận lợi cho biến cố A: “Học sinh được chọn là nam" là: 12+ 4+ 5 = 21 Vậy P(A)=2142=12 b) Các kết quả thuận lợi cho biến cố B: “Học sinh được chọn là nữ và yêu thích môn Bóng đá" là 10. Vậy P(B)=1042=521. c) Các kết quả thuận lợi cho biến cố C: “Học sinh được chọn là nam và yêu thích môn Bóng bàn hoặc Bóng rổ" là:4 + 5 = 9. Vậy P(C)=942=314..
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|