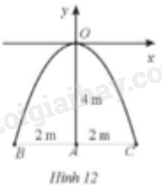
Giải bài 37 trang 73 sách bài tập toán 9 - Cánh diều tập 2Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng (y = a{x^2}), gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng? Đề bài Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng \(y = a{x^2}\), gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?
Phương pháp giải - Xem chi tiết Bước 1: Tìm a (dựa vào điểm \(C\left( {2; - 4} \right)\) thuộc đồ thị hàm số). Bước 2: Ta thấy chiều ngang p là \(p = \left| {2x} \right|\) và khoảng cách từ nóc xe đến điểm cao nhất của cổng là 1m nên \(\left| { - {{\left( {\frac{p}{2}} \right)}^2}} \right| < 1\). Từ đó tìm được p. Lời giải chi tiết Dựa vào đồ thị ta thấy: Điểm \(C\left( {2; - 4} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta có \( - 4 = a{.2^2}\) Hay \(a = - 1\). Suy ra hàm số có dạng \(y = - {x^2}\). Gọi \(K\left( {0; - 1} \right)\) là điểm thuộc Oy. Để xe tải có chiều cao 3 m có chiều ngang p (tức là \(p = \left| {2x} \right|\)) đi vào chính giữa cổng mà không chạm vào cổng thì \(\left| { - {{\left( {\frac{p}{2}} \right)}^2}} \right| < 1\) hay \({p^2} < 4\). Từ đó suy ra \( - 2 < p < 2\). Vậy \( - 2 < p < 2\) là giá trị cần tìm.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
