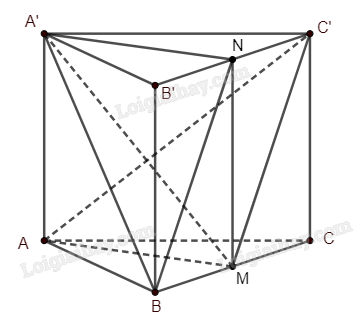
Giải bài 37 trang 112 sách bài tập toán 11 - Cánh diềuCho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\). Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\). Khẳng định nào sau đây là đúng? A. \(\left( {A'MN} \right)\parallel \left( {ACC'} \right)\) B. \(\left( {A'BN} \right)\parallel \left( {AC'M} \right)\) C. \(C'M\parallel \left( {A'B'B} \right)\) D. \(BN\parallel \left( {ACC'A'} \right)\) Phương pháp giải - Xem chi tiết Sử dụng các tính chất về đường thẳng song song với mặt phẳng, các tính chất về hai mặt phẳng song song. Lời giải chi tiết
Ta nhận xét rằng \(A' \in \left( {A'MN} \right)\) và \(A' \in \left( {ACC'A'} \right)\), nên hai mặt phẳng \(\left( {A'MN} \right)\) và \(\left( {ACC'} \right)\) có điểm chung, tức là chúng không song song với nhau. Xét hai mặt phẳng \(\left( {A'BN} \right)\) và \(\left( {AC'M} \right)\). Do \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(B'C'\), nên ta có \(BM = C'N = \frac{1}{2}BC\). Hơn nữa, do \(BC\parallel B'C'\) nên tứ giác \(BMC'N\) là hình bình hành. Suy ra \(BN\parallel C'M\), mà do \(C'M \subset \left( {AC'M} \right)\) nên \(BN\parallel \left( {AC'M} \right)\). Mặt khác, vì \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(B'C'\) nên \(MN\parallel BB'\) và \(MN = BB'\). Do \(ABC.A'B'C'\) là lăng trụ tam giác, nên \(BB'\parallel AA'\) và \(BB' = AA'\). Từ đó ta có \(MN = AA'\) và \(MN\parallel AA'\). Điều này có nghĩa tứ giác \(A'NMA\) là hình bình hành. Suy ra \(A'N\parallel AM\). Do \(AM \subset \left( {AC'M} \right)\) nên \(A'N\parallel \left( {AC'M} \right)\). Vậy \(\left( {A'BN} \right)\parallel \left( {AC'M} \right)\). Xét mặt phẳng \(\left( {BCC'B'} \right)\), ta thấy rằng \(BB'\) và \(CM\) cắt nhau, mà do \(BB' \subset \left( {A'B'B} \right)\) nên \(CM\) và \(\left( {A'B'B} \right)\) có điểm chung, tức là chúng không song song với nhau. Chứng minh tương tự, ta cũng suy ra \(BN\) và \(\left( {ACC'A'} \right)\) không song song với nhau. Đáp án đúng là B.
|