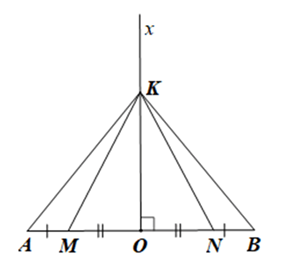
Giải Bài 34 trang 78 sách bài tập toán 7 - Cánh diềuCho điểm M nằm giữa hai điểm O và A. Vẽ các điểm N và B sao cho O là trung điểm của AB và MN. Vẽ tia Ox vuông góc với AB, trên tia Ox lấy điểm K. Chứng minh: Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho điểm M nằm giữa hai điểm O và A. Vẽ các điểm N và B sao cho O là trung điểm của AB và MN. Vẽ tia Ox vuông góc với AB, trên tia Ox lấy điểm K. Chứng minh: a) ∆KOM = ∆KON; b) ∆KMA = ∆KNB. Phương pháp giải - Xem chi tiết - Xét các điều kiện về cạnh và góc để chứng minh ∆KOM = ∆KON và ∆KMA = ∆KNB theo trường hợp cạnh – góc – cạnh. Lời giải chi tiết a) Xét ∆KOM và ∆KON có: \(\widehat {K{\rm{O}}M} = \widehat {K{\rm{O}}N}\) (cùng bằng 90°), OK là cạnh chung, OM = ON (do O là trung điểm của MN). Suy ra ∆KOM = ∆KON (hai cạnh góc vuông). Vậy ∆KOM = ∆KON. b) Do ∆KOM = ∆KON (chứng minh câu a). Suy ra: \(\widehat {KMO} = \widehat {KNO}\) (hai góc tương ứng) và KM = KN (hai cạnh tương ứng). Ta có OA = OM +MA, OB = ON + NB, OA = OB. Suy ra MA = NB. Ta có :\(\widehat {KMO} + \widehat {KMA} = 180^\circ \) (hai góc kề bù) và \(\widehat {KNO} + \widehat {KNB} = 180^\circ \) (hai góc kề bù). Mà \(\widehat {KMO} = \widehat {KNO}\) (chứng minh trên). Suy ra \(\widehat {KMA} = \widehat {KNB}\). Xét ∆KMA và ∆KNB có: MA = NB (chứng minh trên), \(\widehat {KMA} = \widehat {KNB}\) (chứng minh trên), KM = KN (chứng minh trên) Suy ra ∆KMA = ∆KNB (c.g.c). Vậy ∆KMA = ∆KNB.
|