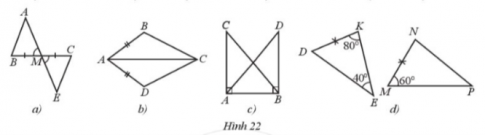
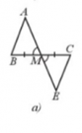
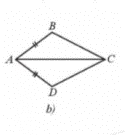
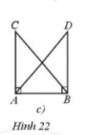
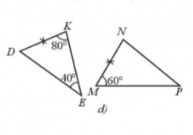
Giải Bài 32 trang 78 sách bài tập toán 7 - Cánh diềuNêu thêm một điều kiện để hai tam giác trong mỗi hình 22a, 22b, 22c, 22d là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Nêu thêm một điều kiện để hai tam giác trong mỗi hình 22a, 22b, 22c, 22d là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh. a) ∆MAB = ∆MEC (Hình 22a). b) ∆BAC = ∆DAC (Hình 22b). c) ∆CAB = ∆DBA (Hình 22c). d) ∆KDE = ∆NMP (Hình 22d). Phương pháp giải - Xem chi tiết Quan sát các hình để thêm các điều kiện để hai tam giác bằng nhau trong trường hợp: cạnh – góc – cạnh. Lời giải chi tiết a) Hình a: Để ΔMAB = ΔMEC theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh. Mà tam giác này có \(\widehat {AMB} = \widehat {CME}\) (hai góc đối đỉnh) và MB = MC. Mặt khác ˆAMBAMB^ là góc xen giữa hai cạnh MA và MB, \(\widehat {CME}\) là góc xen giữa hai cạnh MC và ME. Do đó điều kiện còn lại là điều kiện về cạnh, đó là MA = ME. Vậy Hình 22a cần thêm điều kiện MA = ME. b) Hình b Để ΔBAC = ΔDAC theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh. Mà hai tam giác này có cạnh AC là cạnh chung, AB = AD. Mặt khác \(\widehat {BAC}\) là góc xen giữa hai cạnh AB và AC, \(\widehat {DAC}\) là góc xen giữa hai cạnh AD và AC. Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {BAC} = \widehat {DAC}\). Vậy Hình 22b cần thêm điều kiện \(\widehat {BAC} = \widehat {DAC}\). c) Hình c Để ∆CAB = ∆DBA theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh. Mà hai tam giác này có AB là cạnh chung, \(\widehat {BAC} = \widehat {ABD} = 90^\circ \). Mặt khác ˆBACBAC^ là góc xen giữa hai cạnh AB và AC, \(\widehat {ABD}\) là góc xen giữa hai cạnh BD và BA. Do đó điều kiện còn lại là điều kiện về cạnh, đó là AC = BD. Vậy Hình 22c cần thêm điều kiện AC = BD. d) Hình d Xét ∆KDE có: \(\hat K + \hat D + \hat E = 180^\circ \) (tổng ba góc trong một tam giác). Suy ra \(\hat D = 180^\circ - \hat K - \hat E = 180^\circ - 80^\circ - 40^\circ = 60^\circ \) Để ∆KDE = ∆NMP theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh. Mà DK = NM, \(\hat D = \hat M\) (cùng bằng 60°). Mặt khác \(\hat D\) là góc xen giữa hai cạnh DK và DE, \(\hat M\) là góc xen kẽ giữa hai cạnh MN và MP. Do đó điều kiện còn lại là điều kiện về cạnh, đó là DE = MP. Vậy Hình 2d cần thêm điều kiện DE = MP.
|