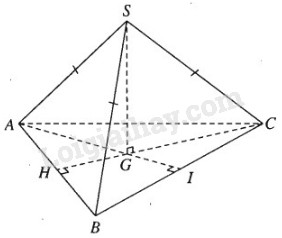
Bài 3.39 trang 160 SBT hình học 11Giải bài 3.39 trang 160 sách bài tập hình học 11. Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC... Đề bài Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC. a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC). b) Tính khoảng cách giữa hai đường thẳng AB và SG Quảng cáo  Lời giải chi tiết
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có SG2=SA2−AG2=(2a)2−[23(3a√32)]2=4a2−3a2=a2 Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a b) Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó HG=13HC mà HC=3a√32 nên HG=a√32. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.
|
