Bài 3.37 trang 160 SBT hình học 11Bài 3.37 trang 160 sách bài tập hình học 11. Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a. Lời giải chi tiết
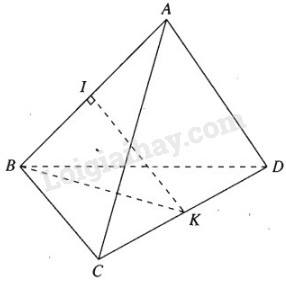
Giả thiết cho ABCD là tứ diện đều nên các cặp cạnh đối diện của tứ diện đó có vai trò như nhau. Do đó ta chỉ cần tính khoảng cách giữa hai cạnh AB và CD là đủ. Gọi I và K lần lượt là trung điểm của AB và CD. Tam giác BCD và ACD đều cạnh a nên hai đường trung tuyến \(BK = AK = \dfrac{{a\sqrt 3 }}{2}\) hay tam giác ABK cân tại K. I là trung điểm AB nên \(KI \bot AB\). Tương tự ta có \(IK \bot CD\). Do đó IK là đoạn vuông góc chung của AB và CD nên nó chính là khoảng cách giữa AB và CD. Tam giác BKI vuông tại I. Ta có : \(I{K^2} = B{K^2} - B{I^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2} = {{{a^2}} \over 2}\) Vậy \(IK = {{a\sqrt 2 } \over 2}\). HocTot.Nam.Name.Vn
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|