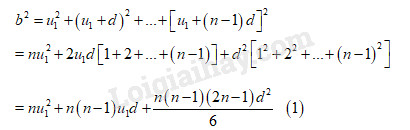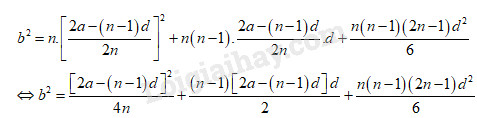Bài 3.22 trang 124 SBT đại số và giải tích 11Giải bài 3.22 trang 124 sách bài tập đại số và giải tích 11. Tìm cấp số cộng biết...
Lựa chọn câu để xem lời giải nhanh hơn
Tìm cấp số cộng \(\left( {{u_n}} \right)\) biết LG a \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 27\\u_1^2 + u_2^2 + u_3^2 = 275\end{array} \right.\) Phương pháp giải: Sử dụng tính chất \({u_{k - 1}} + {u_{k + 1}} = 2{u_k}\). Lời giải chi tiết: Đặt \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 27{\rm{ }}\left( 1 \right)\\u_1^2 + u_2^2 + u_3^2 = 275{\rm{ }}\left( 2 \right)\end{array} \right.\) Ta có: \(\begin{array}{l} Thay \({u_2} = 9\) vào (1) và (2) ta được \(\left\{ \begin{array}{l}{u_1} + {u_3} = 18\,\,(3)\\u_1^2 + u_3^2 = 194\,\,(4)\end{array} \right.\) \(\left( 3 \right) \Rightarrow {u_3} = 18 - {u_1}\) thay vào (4) ta được: \(\begin{array}{l}u_1^2 + {\left( {18 - {u_1}} \right)^2} = 194\\ \Leftrightarrow u_1^2 + 324 - 36{u_1} + u_1^2 = 194\\ \Leftrightarrow 2u_1^2 - 36{u_2} + 130 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{u_1} = 5\\{u_1} = 13\end{array} \right.\end{array}\) Với \({u_1} = 5 \Rightarrow {u_3} = 13\) ta có CSC \(5;9;13\) Với \({u_1} = 13 \Rightarrow {u_3} = 5\) ta có CSC \(13;9;5\). Vậy ta có hai cấp số cộng \(5,9,13\) và \(13,9,5.\) LG b \(\left\{ \begin{array}{l}{u_1} + {u_2} + ... + {u_n} = a\\u_1^2 + u_2^2 + ... + u_n^2 = {b^2}\end{array} \right.\). Phương pháp giải: Sử dụng công thức \({u_n} = {u_1} + \left( {n - 1} \right)d\). Lời giải chi tiết: Ta có:
Mặt khác, \(a = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}\) \( \Rightarrow 2a = 2n{u_1} + \left( {n - 1} \right)d\) \( \Leftrightarrow {u_1} = \dfrac{{2a - \left( {n - 1} \right)d}}{{2n}}\). Thay \({u_1}\) vào (1) ta được:
Kết quả \(d = \pm \sqrt {\dfrac{{12\left( {n{b^2} - {a^2}} \right)}}{{{n^2}\left( {{n^2} - 1} \right)}}} \);\({u_1} = \dfrac{1}{n}\left[ {a - \dfrac{{n\left( {n - 1} \right)}}{2}d} \right]\) HocTot.Nam.Name.Vn
|