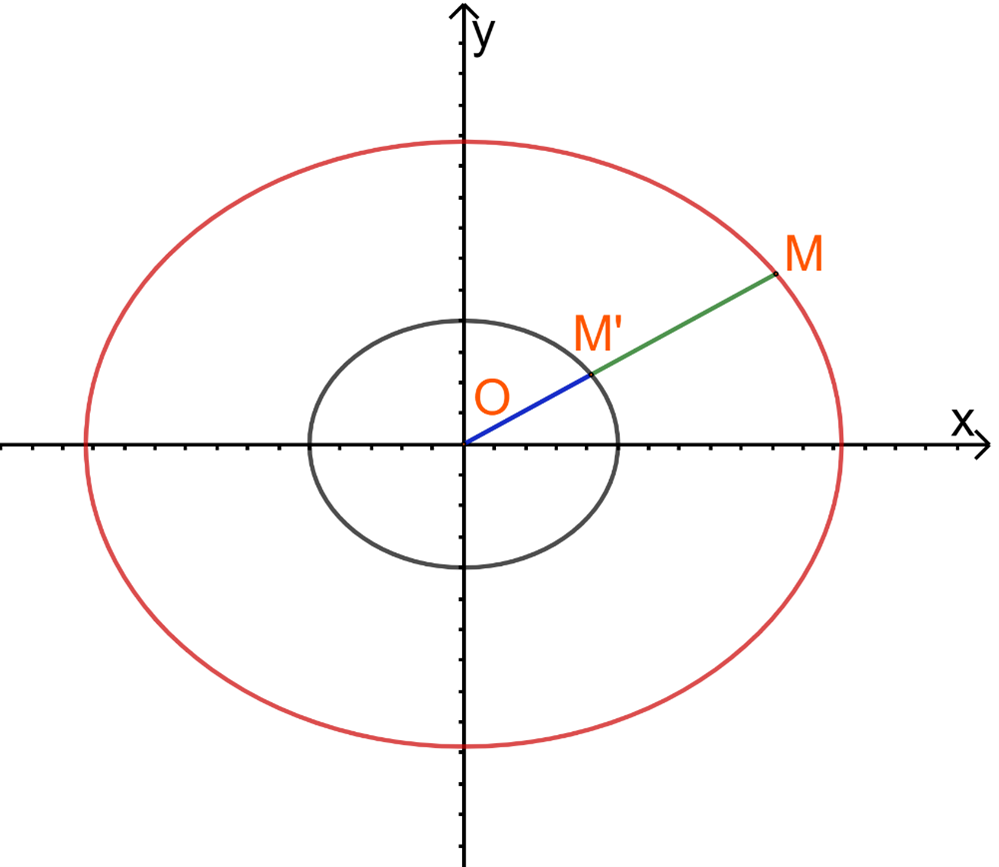
Giải bài 3.20 trang 60 Chuyên đề học tập Toán 10 - Kết nối tri thức với cuộc sốngQuỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu điểm, có tâm sai bằng 0,967. Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Quỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu điểm, có tâm sai bằng 0,967. a) Giải thích vì sao ta có thể coi bất kì hình vẽ elip nào với tâm sai bằng 0,967 là hình ảnh thu nhỏ của quỹ đạo sao chổi Halley. b) Biết khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng \({88.10^6}\) km, tính khoảng cách xa nhất (theo nssdc.gsfc.nasa.gov). Phương pháp giải - Xem chi tiết a) Bước 1: Gọi (E) và (E’) là 2 elip có cùng tâm sai. Bước 2: Lấy M bất kì thuộc (E), chỉ ra tồn tại M’ thuộc (E’) thỏa mãn: \(\overrightarrow {OM'} = \frac{1}{k}\overrightarrow {OM} \) b) Với \(M({x_0};{y_0})\) bất kì thuộc (E), ta có: \(M{F_1}\) nhỏ nhất bằng \(a - c = {88.10^6}\) \(M{F_1}\) lớn nhất bằng \(a + c\) Lời giải chi tiết a) Giả sử quỹ đạo chuyển động của sao chổi Halley có phương trình chính tắc: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (E) Gọi (E’) là elip bất kì với tâm sai \(e' = e = 0,967\), có PTCT: \(\frac{{{x^2}}}{{a{'^2}}} + \frac{{{y^2}}}{{b{'^2}}} = 1\) (a’<a) \(e' = e\) hay \(\frac{{c'}}{{a'}} = \frac{c}{a} \Leftrightarrow \frac{{\sqrt {a{'^2} - b{'^2}} }}{{a'}} = \frac{{\sqrt {{a^2} - {b^2}} }}{a}\) \( \Leftrightarrow \frac{{a{'^2} - b{'^2}}}{{a{'^2}}} = \frac{{{a^2} - {b^2}}}{{{a^2}}} \Leftrightarrow 1 - \frac{{b{'^2}}}{{a{'^2}}} = 1 - \frac{{{b^2}}}{{{a^2}}} \Leftrightarrow \frac{{b'}}{{a'}} = \frac{b}{a} \Leftrightarrow \frac{b}{{b'}} = \frac{a}{{a'}} = k\) (k>1) Lấy \(M({x_0};{y_0})\) bất kì thuộc (E) ta có: \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1 \Leftrightarrow \frac{{{x_0}^2}}{{{{\left( {ka'} \right)}^2}}} + \frac{{{y_0}^2}}{{{{\left( {kb'} \right)}^2}}} = 1 \Leftrightarrow \frac{{{{\left( {\frac{{{x_0}}}{k}} \right)}^2}}}{{a{'^2}}} + \frac{{{{\left( {\frac{{{y_0}}}{k}} \right)}^2}}}{{b{'^2}}} = 1\) \( \Rightarrow M'(\frac{1}{k}{x_0};\frac{1}{k}{y_0}) \in (E')\) Dễ thấy \(\overrightarrow {OM'} = \frac{1}{k}\overrightarrow {OM} \) với mọi M thuộc (E) Nói cách khác, (E’) là một elip thu nhỏ của (E).
b) Giả sử tâm Mặt Trời ở vị trí tiêu điểm \({F_1}( - c;0)\) Với \(M({x_0};{y_0})\) bất kì thuộc (E), ta có: \(M{F_1}\) nhỏ nhất bằng \(a - c = {88.10^6}\) Mà \(e = \frac{c}{a} = 0,967\) \( \Rightarrow \left\{ \begin{array}{l}a = \frac{8}{3}{.10^9} \approx 2\;666\;666\;667\\c \approx 2\;578\;666\;667\end{array} \right.\) \( \Rightarrow \)\(M{F_1}\) lớn nhất bằng \(a + c = 5\;245\;333\;334\) (km). Vậy khoảng cách xa nhất từ sao chổi Halley đến tâm Mặt trời là 5 245 333 334 km.
|