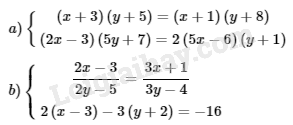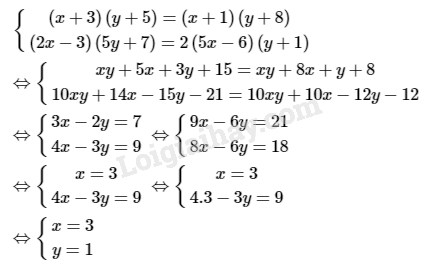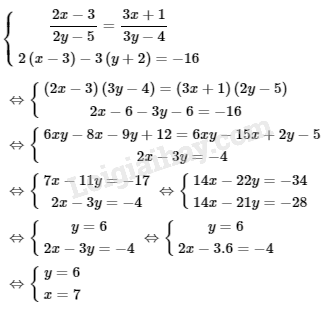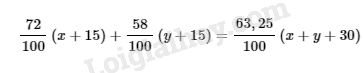Bài 3.1, 3.2, 3.3, 3.4 phần bài tập bổ sung trang 16 SBT toán 9 tập 2

Bài III.1

Giải các hệ phương trình:

Phương pháp giải:

Sử dụng:

- Biến đổi hệ phương trình đã cho về hệ hai phương trình bậc nhất hai ẩn.

- Cách giải hệ phương trình bằng phương pháp cộng đại số:

+ Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.

+ Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).

+ Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

Lời giải chi tiết:

\(a)\)

Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) =  (3; 1)\).

\(b)\) Điều kiện: \(y \ne \displaystyle{5 \over 2};y \ne \displaystyle{4 \over 3}\)

Ta thấy \(x=7;y=6\) thoả mãn điều kiện bài toán.

Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) =  (7; 6)\).

Bài III.2

Năm nay người ta áp dụng kĩ thuật mới trên hai cánh đồng trồng lúa ở ấp Minh Châu. Vì thế lượng lúa thu được trên cánh đồng thứ nhất tăng lên 30% so với năm ngoái, trên cánh đồng thứ hai lượng lúa thu được tăng 20%. Tổng cộng cả hai cánh đồng thu được \(630\) tấn. Hỏi trên mỗi cánh đồng năm nay thu được bao nhiêu lúa, biết rằng trên cả hai cánh đồng này năm ngoái chỉ thu được \(500\) tấn?

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết:

Gọi khối lượng lúa thu được năm ngoái trên cánh đồng thứ nhất và cánh đồng thứ hai lần lượt là \(x\) (tấn), \(y\) (tấn).

Điều kiện: \(x > 0; y > 0\)

Năm ngoái trên cả hai cánh đồng lượng lúa thu được là \(500\) tấn, ta có phương trình:

\(x + y = 500\)

Lượng lúa thu được năm nay trên cánh đồng thứ nhất tăng lên 30% so với năm ngoái tức là tăng \(\displaystyle{3 \over {10}}x\) (tấn)

Lượng lúa thu được năm nay trên cánh đồng thứ hai tăng lên 20% so với năm ngoái tức là tăng \(\displaystyle{2 \over {10}}y\) (tấn)

Năm nay lượng lúa trên cả hai cánh đồng tăng được \(630 – 500 = 130\) tấn, ta có phương trình:

\(\displaystyle{3 \over {10}}x + {2 \over {10}}y = 130\)

Ta có hệ phương trình:

\(\eqalign{
& \left\{ {\matrix{
{x + y = 500} \cr 
{\displaystyle{3 \over {10}}x + {2 \over {10}}y = 130} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{x + y = 500} \cr 
{3x + 2y = 1300} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{2x + 2y = 1000} \cr 
{3x + 2y = 1300} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{x = 300} \cr 
{x + y = 500} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{x = 300} \cr 
{y = 200} \cr} } \right. \cr} \)

Giá trị \(x = 300; y = 200\) thỏa mãn điều kiện bài toán.

Vậy năm nay trên cánh đồng thứ nhất thu được: \(x+\displaystyle{3 \over {10}}x=300 + \displaystyle{{3} \over {10}}.300 = 390\) tấn.

Năm nay trên cánh đồng thứ hai thu được: \(630 – 390 = 240\) tấn.

Bài III.3

Người ta trộn hai loại quặng sắt với nhau, một loại chứa 72% sắt, loại thứ hai chứa 58% sắt được một loại quặng chứa 62%  sắt. Nếu tăng khối lượng của mỗi loại quặng thêm \(15\) tấn thì được một loại quặng chứa 63,25% sắt. Tìm khối lượng quặng của mỗi loại đã trộn.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết:

Gọi khối lượng quặng loại thứ nhất là \(x\) (tấn), loại thứ hai là \(y\) (tấn).

Điều kiện: \(x > 0; y > 0\)

Lượng sắt nguyên chất có trong mỗi loại quặng bằng lượng sắt có trong hỗn hợp nên ta có phương trình:

\(\displaystyle{{72} \over {100}}x + {{58} \over {100}}y = {{62} \over {100}}\left( {x + y} \right)\)

Nếu tăng khối lượng của mỗi loại quặng thêm \(15\) tấn thì được một loại quặng chứa 63,25% sắt, khi đó ta có phương trình:

Ta có hệ phương trình:

Cả hai giá trị \(x = 12; y = 30\) thỏa mãn điều kiện bài toán.

Vậy khối lượng quặng loại thứ nhất là \(12\) tấn, loại thứ hai là \(30\) tấn.

Bài III.4

Một người đi ngựa và một người đi bộ đều đi từ bản \(A\) đến bản \(B\). Người đi ngựa đến \(B\) trước người đi bộ \(50\) phút rồi lập tức quay trở về \(A\) và gặp người đi bộ tại một địa điểm cách \(B\) là \(2km\). Trên cả quãng đường từ \(A\) đến \(B\) và ngược lại, người đi ngựa đi hết \(1\) giờ \(40\) phút. Hãy tính khoảng cách \(AB\) và vận tốc của mỗi người.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước \(1\): Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước \(2\): Giải hệ phương trình nói trên.

Bước \(3\): Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Công thức tính quãng đường đi được: \(S=v.t;\)

Trong đó \(S\) là quãng đường đi được \((km)\); \(v\) là vận tốc \((km/h)\); \(t\) là thời gian \((h)\).

Lời giải chi tiết:

Gọi khoảng cách giữa hai bản \(A\) và \(B\) là \(x \ (km)\), vận tốc của người đi bộ là \(y \ (km/h)\).

Điều kiện: \(x > 0; y > 0\)

Đổi \(1\) giờ \(40\) phút \( = \displaystyle{5 \over 3} \) giờ

Người đi ngựa đi từ \(A\) đến \(B\) và ngược lại hết \(  \displaystyle{5 \over 3} \ (h)\) nên người đi ngựa đi từ \(A\) đến \(B\) hết \(\displaystyle{5 \over 3}:2 = {5 \over 6} \ (h)\) .

Vận tốc của người đi ngựa là \(\displaystyle x:{5 \over 6} = {6 \over 5}x (km/h)\)

Thời gian người đi bộ đi hết quãng đường \(AB\) là \(\displaystyle{x \over y} \ (h)\) 

Người đi ngựa đến \(B\) trước người đi bộ  \(50\) phút tức là \( \displaystyle{5 \over 6}\) giờ, ta có phương trình:

\(\displaystyle{x \over y} - {5 \over 6} = {5 \over 6} \Leftrightarrow \displaystyle{x \over y} = {5 \over 3} \\ \Leftrightarrow3x = 5y \ \  (1)\)

Từ \((1)\) suy ra \( 6x = 10y\)\( \Leftrightarrow \displaystyle{6 \over 5}x = 2y.\) Điều này có nghĩa là vận tốc của người đi ngựa gấp đôi vận tốc của người đi bộ hay vận tốc của người đi ngựa là \(2y (km/h).\)

Từ lúc đi đến lúc gặp nhau người đi bộ đi được \(x – 2 (km)\), người đi ngựa đi được \(x + 2 (km).\)

Vì từ lúc đi đến lúc gặp nhau thời gian hai người đi bằng nhau nên ta có phương trình:

\(\eqalign{
& {{x - 2} \over y} = {{x + 2} \over {2y}} \cr 
& \Leftrightarrow 2x - 4 = x + 2 \cr} \)

Ta có hệ phương trình:

\(\eqalign{
& \left\{ {\matrix{
{3x = 5y} \cr 
{2x - 4 = x + 2} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{3x = 5y} \cr 
{x = 6} \cr} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{3.6 = 5y} \cr 
{x = 6} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{x = 6} \cr 
{y = 3,6} \cr} } \right. \cr} \)

Ta thấy \(x = 6\) và \(y = 3,6\)  thỏa mãn điều kiện bài toán.

Vậy khoảng cách \(AB\) là \(6km\), vận tốc của người đi bộ là \(3,6 \  km/h\), vận tốc của người đi ngựa là \(7,2 \,km/h\).

HocTot.Nam.Name.Vn