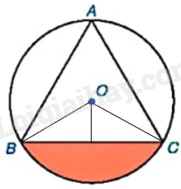
Giải bài 3 trang 95 vở thực hành Toán 9 tập 2Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như hình bên. a) Tính bán kính R của đường tròn (O). b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như hình bên.
a) Tính bán kính R của đường tròn (O). b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC. Phương pháp giải - Xem chi tiết a) Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\). b) + Tính S’ là diện tích hình quạt chắn cung nhỏ BC, tính diện tích tam giác BOC. + Khi đó, \(S = S' - {S_{BOC}}\). Lời giải chi tiết a) Ta có: \(R = \frac{{\sqrt 3 }}{3}BC = \sqrt 3 \left( {cm} \right)\). b) Bán kính đường tròn nội tiếp tam giác ABC là: \(r = \frac{{\sqrt 3 }}{6}BC = \frac{{\sqrt 3 }}{2}\left( {cm} \right)\). Chiều cao từ đỉnh O xuống cạnh BC của \(\Delta BOC\) bằng bán kính đường tròn nội tiếp tam giác ABC. Do vậy, \({S_{BOC}} = \frac{1}{2}r.BC = \frac{1}{2}.\frac{{\sqrt 3 }}{2}.3 = \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)\). Ta có: \(\widehat {BOC} = 2.\widehat {BAC} = {120^o}\). Diện tích hình quạt chắn cung nhỏ BC là: \(S' = \frac{{120}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \pi \left( {c{m^2}} \right)\). Diện tích hình viên phân cần tính là: \(S = S' - {S_{BOC}} = \pi - \frac{{3\sqrt 3 }}{4} \approx 1,84\left( {c{m^2}} \right)\).  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
