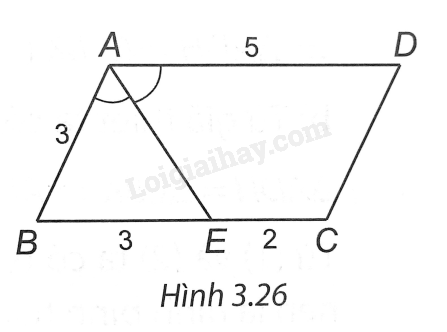
Giải bài 3 trang 55 vở thực hành Toán 8

Đề bài

Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.

a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

b) Tính khoảng cách từ giao điểm đó đến điểm C.

Lời giải chi tiết

(H.3.26). a) Do ABCD là hình bình hành nên AD // BC, BC = AD = 5 cm.

Do BC = 5 cm nên có điểm E duy nhất trên cạnh BC sao cho BE = 3 cm.

Vì BE = AB ⇒ ∆BAE cân tại B \( \Rightarrow \widehat {BAE} = \widehat {BEA}.\) (1)

Do AD // BC \( \Rightarrow \widehat {BEA} = \widehat {EAD}\) (hai góc so le trong). (2)

Từ (1) và (2), ta có \(\widehat {BAE} = \widehat {EAD}\) hay tia AE là tia phân giác của góc BAD. Tia này không cắt cạnh CD.

b) Ta có EC = BC – BE = 5 – 3 = 2 (cm).