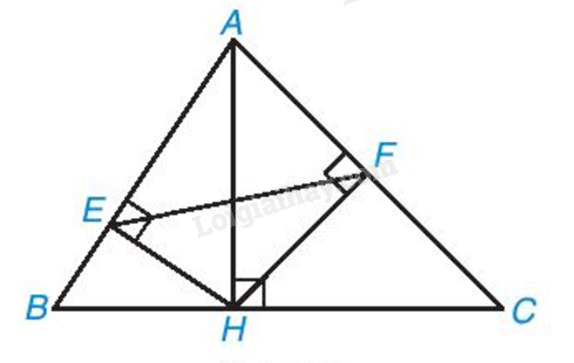
Giải bài 3 trang 102 vở thực hành Toán 8 tập 2Trong hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Trong hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng a) ΔAEH ∽ ΔAHB b) ΔAFH ∽ ΔAHC c) ΔAFE ∽ ΔABC
Phương pháp giải - Xem chi tiết Sử dụng các trường hợp đồng dạng của tam giác vuông và tam giác thường. Lời giải chi tiết a) Hai tam giác vuông AEH (vuông tại E) và AHB (vuông tại H) có $\widehat{EAH}=\widehat{HAB}$ (góc chung). Do đó $\Delta AEH\backsim \Delta AHB$ (một cặp góc nhọn bằng nhau). b) Hai tam giác vuông AFH (vuông tại F) và AHC (vuông tại H) có $\widehat{FAH}=\widehat{HAC}$ (góc chung). Do đó $\Delta AFH\backsim \Delta AHC$ (một cặp góc nhọn bằng nhau). c) Vì $\Delta AEH\backsim \Delta AHB$ nên \(\frac{AE}{AC}=\frac{AE}{AH}.\frac{AH}{AC}=\frac{AH}{AB}.\frac{AH}{AC}=\frac{A{{H}^{2}}}{AB.AC}\) (1) Vì $\Delta AFH\backsim \Delta AHC$ nên \(\frac{AF}{AB}=\frac{AF}{AH}.\frac{AH}{AB}=\frac{AH}{AC}.\frac{AH}{AB}=\frac{A{{H}^{2}}}{AB.AC}\) (2) Từ (1) và (2) suy ra $\frac{AE}{AC}=\frac{AF}{AB}$. Hai tam giác AFE và ABC có $\widehat{A}$ chung; $\frac{AE}{AC}=\frac{AF}{AB}$ (Theo chứng minh trên). Do đó \(\Delta AFE\backsim \Delta ABC\) (c.g.c).
|