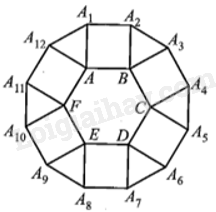
Giải bài 28 trang 114 sách bài tập toán 9 - Cánh diều tập 2Cho lục giác đều ABCDEF. Về phía ngoài lục giác dựng các hình vuông BAA1A2, CBA3A4, DCA5A6, EDA7A8, FEA9A10, AFA11A12. Đa giác A1A2A3…A11A12 có phải là đa giác đều không? Vì sao? Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho lục giác đều ABCDEF. Về phía ngoài lục giác dựng các hình vuông BAA1A2, CBA3A4, DCA5A6, EDA7A8, FEA9A10, AFA11A12. Đa giác A1A2A3…A11A12 có phải là đa giác đều không? Vì sao? Phương pháp giải - Xem chi tiết Dựa vào: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Lời giải chi tiết
Vì ABCDEF là lục giác đều nên nó có tất các cạnh bằng nhau và tất cả các góc đều bằng \(\frac{{{{2.360}^o}}}{6} = {120^o}\). Ta có \(\widehat {ABC} + \widehat {AB{A_2}} + \widehat {{A_2}B{A_3}} + \widehat {CB{A_3}} = {360^o}\). Suy ra: \(\widehat {{A_2}B{A_3}} = {360^o} - \widehat {ABC} - \widehat {AB{A_2}} - \widehat {CB{A_3}}\) \(= {360^o} - {120^o} - {90^o} - {90^o} = {60^o}\). Do BA2 = AB (do BAA1A2 là hình vuông); BA3 = BC (do CBA3A4) và AB = CD nên BA2 = BA3. Do đó BA2A3 là tam giác đều. Từ đó suy ra: A2A3 = BA2 và \(\widehat {B{A_2}{A_3}} = {60^o}\). Do đó A2A3 = BA (cùng bằng BA2) và \(\widehat {{A_1}{A_2}{A_3}} = \widehat {{A_1}{A_2}B} + \widehat {B{A_2}{A_3}} = {90^o} + {60^o} = {150^o}\). Tương tự, ta chứng minh được đa giác A1A2A3…A11A12 có các góc đều bằng 150° và các cạnh đều bằng nhau và bằng BA. Do đó, đa giác A1A2A3…A11A12 là đa giác đều.
|