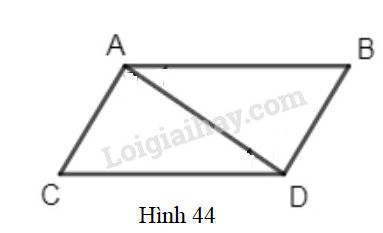
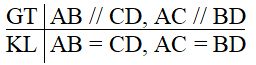Bài 25 trang 127 Vở bài tập toán 7 tập 1Giải bài 25 trang 127 VBT toán 7 tập 1. Trên hình 44 ta có AB//CD, AC//BD. Hãy chứng minh rằng AB=CD,AC=BD. Đề bài Trên hình 44 ta có AB//CD,AC//BD. Hãy chứng minh rằng: AB=CD;AC=BD. Phương pháp giải - Xem chi tiết Áp dụng: - Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kìa thì hai tam giác đó bằng nhau. - Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc so le trong bằng nhau. Lời giải chi tiết
Nối AD. Vì AB // CD nên ^DAB=^ADC ( 2 góc so le trong) Vì AC // BD nên ^ADB=^DAC ( 2 góc so le trong) Xét ∆ADB và ∆DAC có: \widehat {DAB} = \widehat {ADC} AD là cạnh chung \widehat {ADB} = \widehat {DAC} Do đó ∆ADB=∆DAC (g.c.g) suy ra AB=CD, BD=AC (hai cạnh tương ứng) HocTot.Nam.Name.Vn
|