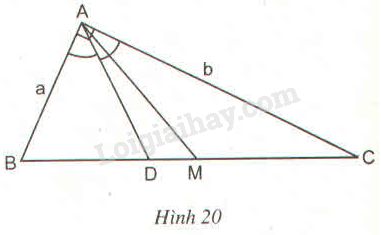
Bài 24 trang 88 SBT toán 8 tập 2Giải bài 24 trang 88 sách bài tập toán 8. Tam giác vuông ABC có góc A = 90^o , AB = a (cm), AC = b (cm), (a < b) ... Đề bài Tam giác vuông ABC có ˆA=90∘, AB=a(cm),AC=b(cm), (a<b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC) (h.20). a) Tính độ dài các đoạn thẳng BC,BD,DC,AM và DM theo a,b. b) Hãy tính các đoạn thẳng trên đây chính xác đến chữ số thập phân thứ hai khi biết a=4,15cm;b=7,25cm.
Phương pháp giải - Xem chi tiết Sử dụng: - Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy. - Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông. - Tính chất: ab=cd⇒aa+b=cc+d Lời giải chi tiết a) Áp dụng định lí Py-ta-go vào tam giác vuông ABC, ta có: BC2=AB2+AC2=a2+b2 ⇒BC=√a2+b2 Ta có: AM=BM=12BC (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy). ⇒AM=12√a2+b2 Vì AD là đường phân giác của ^BAC nên theo tính chất đường phân giác của tam giác ta có: DBDC=ABAC Từ đó, ta có: DBDC=ABAC ⇒DBDB+DC=ABAB+AC ⇒DBBC=ABAB+AC ⇒DB=AB.BCAB+AC=a√a2+b2a+b Vậy DC=BC−DB=√a2+b2−a√a2+b2a+b=b√a2+b2a+b DM=BM−BD=12√a2+b2−a√a2+b2a+b =(a+b)√a2+b2−2a√a2+b22(a+b)=√a2+b2(a+b−2a)2(a+b)=(b−a)√a2+b22(a+b) b) Với a=4,15cm;b=7,25cm, ta tính được: BC=√(4,15)2+(7,25)2≈8,35(cm) BD=4,15√(4,15)2+(7,25)24,15+7,25≈3,04(cm) DC=b√a2+b2a+b≈5,31(cm); AM=12√a2+b2≈4,18(cm); DM=(b−a)√a2+b22(a+b)≈1,14(cm). HocTot.Nam.Name.Vn
|