Bài 2.34 trang 80 SBT hình học 11

Đề bài

Vẽ hình biểu diễn của một hình lục giác đều.

Lời giải chi tiết

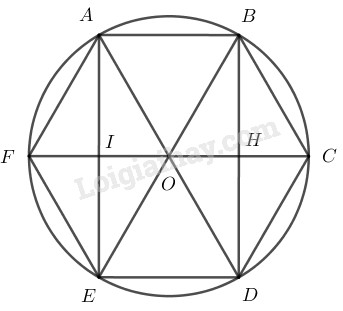
Với hình lục giác đều $ABCDEF$ ta nhận thấy:

- Tứ giác $OABC$ là hình bình hành (vừa là hình thoi);

- Các điểm $D$, $E$, $F$ lần lượt là các điểm đối xứng của các điểm $A$, $B$, $C$ qua tâm $O$.

Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều $ABCDEF$ như sau:

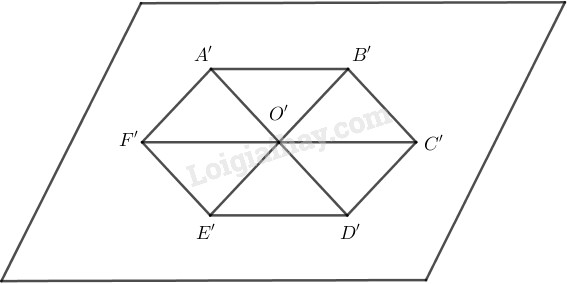
- Vẽ hình bình hành $O’A’B’C’$ biểu diễn cho hình bình hành $OABC$.

- Lấy các điểm $D’$, $E’$, $F’$ lần lượt đối xứng của $A’$, $B’$, $C’$ qua tâm $O’$, ta được hình biểu diễn $A’B’C’D’E’F’$ của hình lục giác đều $ABCDEF$.

Chú ý. Ta có thể vẽ hình biểu diễn hình lục giác đều dựa trên sự phân tích sau đây ở hình thực $ABCDEF$:

- Tứ giác $ABDE$ là hình chữ nhật;

- Gọi $I$ là trung điểm của cạnh $AE$ và $H$ là trung điểm của cạnh $BD$;

- Các điểm $F$ và $C$ đối xứng của $O$ lần lượt qua $I$ và $H$.

Từ đó ta có cách vẽ sau đây:

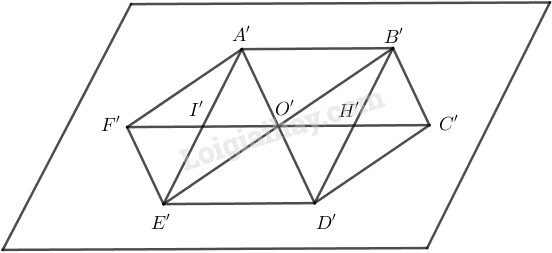
- Vẽ hình bình hành $A’B’D’E’$ biểu diễn cho hình chữ nhật $ABDE$

- Gọi $I’$ và $H’$ lần lượt là trung điểm của $A’E’$và $B’D’$.

- Gọi $F’$ đối xứng với $O’$ qua $I’$ và (C’\) đối xứng với $O’$ qua $H’$, ta được  hình biểu diễn $A’B’C’D’E’F’$ của hình lục giác đều.

 HocTot.Nam.Name.Vn