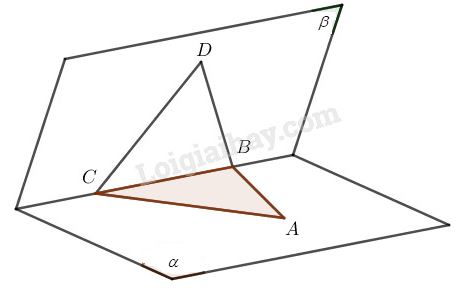
Bài 2.33 trang 80 SBT hình học 11Giải bài 2.33 trang 80 sách bài tập hình học 11. Chứng minh rằng có thể xem tam giác ABC là hình chiếu song song của một tam giác đều nào đó. Đề bài Trong mặt phẳng (α) cho một tam giác ABC bất kì. Chứng minh rằng có thể xem tam giác ABC là hình chiếu song song của một tam giác đều nào đó. Phương pháp giải - Xem chi tiết Sử dụng khái niệm hình chiếu song song của một điểm: Cho mặt phẳng (α) và đường thẳng Δ cắt mặt phẳng (α). Với mỗi điểm M trong không gian, đường thẳng đi qua M và song song hoặc trùng với Δ cắt (α) tại điểm M′ xác định. Điểm M′ được gọi là hình chiếu song song của một điểm M trên mặt phẳng (α) theo phương Δ. Quảng cáo  Lời giải chi tiết Cho tam giác ABC bất kì nằm trong mặt phẳng (α). Gọi (β) là mặt phẳng qua BC và khác với (α). Trong (β) ta vẽ tam giác đều BCD. Vậy ta có thể xem tam giác ABC cho trước là hình chiếu song song của tam giác đều DBC theo phương chiếu DA lên mặt phẳng (α).
HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.
|
