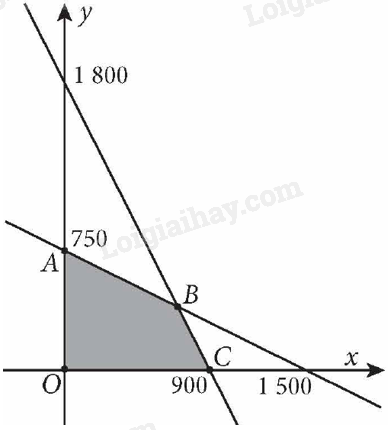
Giải bài 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thứcMột nhà máy hóa chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm3 khí CO (carbon monoxide) và 6 dm3 khí SO2 (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm3 khí CO và 3 dm3 khí SO2 phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm3 khí CO và không quá 5 400 dm3 khí SO2. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồn Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Một nhà máy hóa chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm3 khí CO (carbon monoxide) và 6 dm3 khí SO2 (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm3 khí CO và 3 dm3 khí SO2 phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm3 khí CO và không quá 5 400 dm3 khí SO2. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồng một đơn vị hợp chất X và 24 000 đồng một đơn vị hợp chất Y. Xác định số đơn vị hợp chất X và Y mỗi loại cần sản xuất trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường. Phương pháp giải - Xem chi tiết F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên Lời giải chi tiết Gọi x và y lần lượt là số đơn vị hợp chất X và Y cần sản xuất. Lợi nhuận thu được là: F(x; y) = 36 000x + 24 000y (đồng). Ta có hệ bất phương trình sau: {x≥0,y≥02x+4y≤30006x+3y≤5400 Miền nghiệm của hệ bất phương trình này là miền tứ giác OABC được tô màu như hình vẽ dưới đây:
Các điểm cực biên là: O(0; 0), A(0; 750), B(700; 400), C(900; 0). Ta có: F(0; 0) = 36 000.0 + 24 000.0 = 0; F(0; 750) = 36 000.0 + 24 000.750 = 18 000 000; F(700; 400) = 36 000.700 + 24 000.400 = 34 800 000; F(900; 0) = 36 000.900 + 24 000.0 = 32 400 000. Giá trị lớn nhất của F(x; y) bằng 34 800 tại điểm cực biên B(700; 400). Vậy cần sản xuất 700 đơn vị hợp chất X và 400 đơn vị hợp chất Y trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|