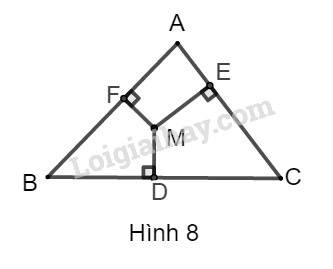
Bài 20 trang 105 SBT toán 9 tập 1Giải bài 20 trang 105 sách bài tập toán 9. Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kể MD, ME, MF lần lượt vuông góc với các cạnh BC, AC, AB Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kẻ MD,ME,MF lần lượt vuông góc với các cạnh BC,AC,AB. Chứng minh rằng: BD2+CE2+AF2=DC2+EA2+FB2.
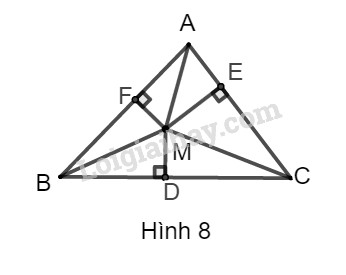
Phương pháp giải - Xem chi tiết - Vẽ hình phụ tạo thành các tam giác vuông (với bài toán này ta nối các điểm tạo thành các cạnh AM,BM,CM). - Xét các tam giác vuông, sử dụng định lý Pytago tạo thành các đẳng thức phù hợp. - Tìm mối liên hệ giữa các đẳng thức vừa được tạo thành và đẳng thức cần được chứng minh của bài toán. Sử dụng: Định lý Pytago: Cho tam giác ABC vuông tại A, ta có: BC2=AB2+AC2 Lời giải chi tiết Nối AM,CM,BM ta được hình dưới đây:
Áp dụng định lí Pytago vào tam giác vuông BDM, ta có: BM2=BD2+DM2⇒BD2=BM2−DM2 (1) Áp dụng đinh lí Pytago vào tam giác vuông CEM, ta có: CM2=CE2+EM2⇒CE2=CM2−EM2 (2) Áp dụng định lí Pytago vào tam giác vuông AFM, ta có: AM2=AF2+FM2⇒AF2=AM2−FM2 (3) Cộng từng vế của (1), (2) và (3) ta có: BD2+CE2+AF2 =BM2−DM2+CM2−EM2+AM2−FM2 (4) Áp dụng định lí Pytago vào tam giác vuông BFM, ta có: BM2=BF2+FM2 (5) Áp dụng định lí Pytago vào tam giác vuông CDM, ta có: CM2=CD2+DM2 (6) Áp dụng định lí Pytago vào tam giác vuông AEM, ta có: AM2=AE2+EM2 (7) Thay (5), (6), (7) vào (4) ta có: BD2+CE2+AF2=BF2+FM2−DM2+CD2+DM2−EM2+AE2+EM2−FM2=DC2+EA2+FB2 Vậy BD2+CE2+AF2=DC2+EA2+FB2. HocTot.Nam.Name.Vn
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|