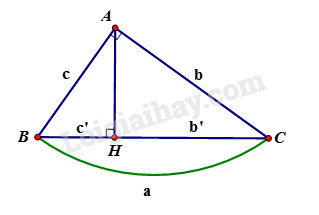
Bài 1.4 phần bài tập bổ sung trang 105 SBT toán 9 tập 1Giải bài 1.4 phần bài tập bổ sung trang 105 sách bài tập toán 9. Hãy biểu thị b', c' qua a, b, c... Đề bài Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH :\) \(AB = c, AC = b, BC = a,\)\( AH = h, BH = c', CH = b'.\) Hãy biểu thị \(b', c'\) qua \(a, b, c\). Phương pháp giải - Xem chi tiết
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau: +) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\) +) \(A{C^2} = CH.BC\) hay \({b^2} = ab'\) Lời giải chi tiết Từ \({b^2} = ab',{c^2} = ac'\) suy ra \(b' = \dfrac{{{b^2}}}{a},c' = \dfrac{{{c^2}}}{a}.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
