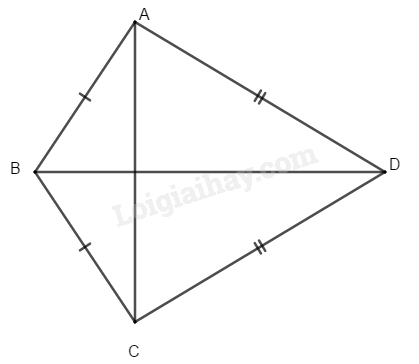
Bài 2 trang 80 SBT toán 8 tập 1Giải bài 2 trang 80 sách bài tập toán 8. Tứ giác ABCD có AB=BC, CD=DA.a) Chứng minh rằng BD là đường trung trực của AC ... Đề bài Tứ giác ABCD có AB=BC,CD=DA. a) Chứng minh rằng BD là đường trung trực của AC b) Cho biết ˆB=1000,ˆD=700 tính ˆA và ˆC. Phương pháp giải - Xem chi tiết a) Sử dụng tính chất đường trung trực của đoạn thẳng. b) Tổng bốn góc của một tứ giác bằng 360o. Lời giải chi tiết
a) Ta có: BA=BC (gt) ⇒ điểm B thuộc đường trung trực của AC Lại có: DA=DC (gt) ⇒ điểm D thuộc đường trung trực của AC B và D là hai điểm phân biệt cùng thuộc đường trung trực của AC nên đường thẳng BD là đường trung trực của AC. b) Xét ∆BAD và ∆BCD, ta có: BA=BC (gt) DA=DC (gt) BD cạnh chung Do đó ∆BAD=∆BCD(c.c.c) ⇒^BAD=^BCD (hai góc tương ứng) Ta có: ^BAD+^BCD+^ABC+^ADC=3600 (tổng 4 góc trong tứ giác) ⇒^BAD+^BAD=3600−(1000+700) ⇒2^BAD=1900 ⇒^BAD=1900:2=950 HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|