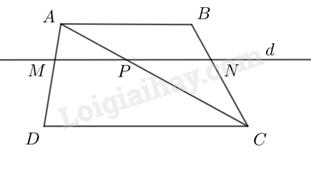
Giải bài 2 trang 57 SGK Toán 8 – Cánh diều

Đề bài

Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.

a)      Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);

b)     Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.

Lời giải chi tiết

a)      Vì \(d\parallel CD\) nên \(MP\parallel CD\)

Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{MD}} = \frac{{AP}}{{PC}}\,\,\left( 1 \right)\) (Định lý Thales)

Vì \(d\parallel AB\) nên \(PN\parallel AB\)

Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{BN}}{{NC}} = \frac{{AP}}{{PC}}\,\,\left( 2 \right)\) (Định lý Thales)

Từ (1) và (2) ta có \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\).

b)     Vì \(MD = 2MA\) nên \(\frac{{AM}}{{MD}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AD}} = \frac{1}{3}\)

Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{AD}} = \frac{{MP}}{{DC}}\) (Hệ quả định lý Thales)

\( \Rightarrow \frac{{MP}}{{DC}} = \frac{1}{3} \Rightarrow MP = \frac{1}{3}DC = 2cm\)

Vì \(\frac{{AM}}{{AD}} = \frac{1}{3} \Rightarrow \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{CA}} = \frac{2}{3}\)

Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{CP}}{{CA}} = \frac{{PN}}{{AB}}\) (Hệ quả định lý Thales)

\( \Rightarrow \frac{{PN}}{{AB}} = \frac{2}{3} \Rightarrow PN = \frac{2}{3}AB = \frac{8}{3}cm\)

Mà \(MN = MP + PM = 2 + \frac{8}{3} = \frac{{14}}{3}cm\).