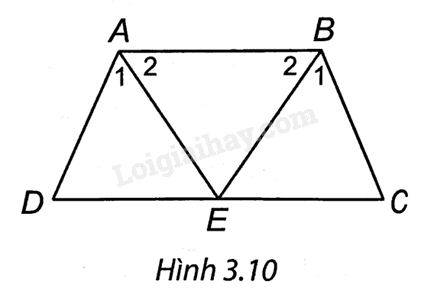
Giải bài 2 trang 48 vở thực hành Toán 8Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED. Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED. Phương pháp giải - Xem chi tiết Sử dụng khái niệm hình thang cân: Hình thang cân là hình cân là hình thang có hai góc kề một đáy bằng nhau. Xét ∆ADE và ∆BCE bằng nhau suy ra EC = ED. Lời giải chi tiết
Hình thang ABCD cân nên \(\widehat {DAB} = \widehat {ABC}\) \( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}}\) Xét ∆ADE và ∆BCE có: \(A{\rm{D}} = BC;\widehat C = \widehat D\) (do hình thang ABCD cân), \(\widehat {{A_1}} = \widehat {{B_1}}\), do đó ∆ADE = ∆BCE (g.c.g), suy ra EC = ED.
|