Giải bài 2 trang 35 vở thực hành Toán 9 tập 2Cho hàm số (y = a{x^2}). Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho hàm số y=ax2. Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó. Phương pháp giải - Xem chi tiết - Thay x=3;y=3 vào hàm số y=ax2 để tìm a. - Cách vẽ đồ thị hàm số y=ax2(a≠0): + Lập bảng ghi một số cặp giá trị tương ứng của x và y. + Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số y=ax2(a≠0). Lời giải chi tiết Thay x=3 và y=3 vào phương trình y=ax2ta có: 3=a.32, suy ra a=13. Lập bảng một số giá trị tương ứng giữa x và y=13x2.
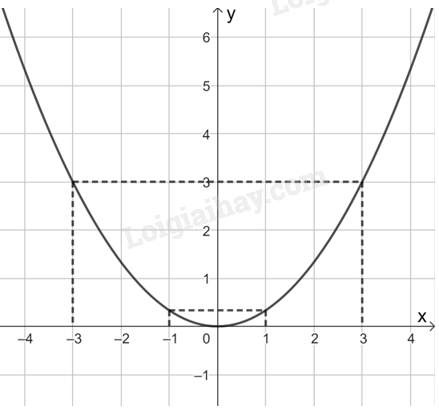
Đồ thị của hàm số y=13x2 như hình sau:
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|