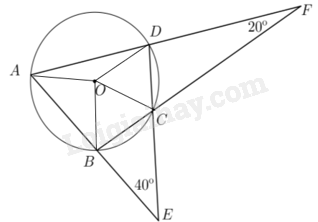
Giải bài 2 trang 106 vở thực hành Toán 9 tập 2Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như hình sau đây. Biết (widehat {BEC} = {40^o}) và (widehat {DFC} = {20^o}), tính số đo các góc của tứ giác ABCD. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như hình sau đây. Biết \(\widehat {BEC} = {40^o}\) và \(\widehat {DFC} = {20^o}\), tính số đo các góc của tứ giác ABCD.
Phương pháp giải - Xem chi tiết + Tính được \(\hat A + \hat D = {180^ \circ } - \widehat E = {140^ \circ }\), suy ra \(\frac{1}{2}\left( {\widehat {BOC} + \widehat {COD}} \right) + \frac{1}{2}\left( {\widehat {AOB} + \widehat {BOC}} \right) = {140^o}\), hay \(\frac{1}{2}\left( {{{360}^o} + \widehat {BOC} - \widehat {AOD}} \right) = {140^o}\) nên \(\widehat {DOA} - \widehat {BOC} = {80^o}\) (1) + Tương tự tính được \(\widehat {AOB} - \widehat {COD} = {40^o}\) (2) + Cộng vế với vế của (1) và (2) ta có: \(\widehat {AOB} + \widehat {DOA} - \widehat {COD} - \widehat {BOC} = {120^o}\) hay , biết \(sđ\overset\frown{DAB}+sđ\overset\frown{BCD}={{360}^{o}}\) + $\widehat{C}=\frac{1}{2}sđ\overset\frown{DAB};\widehat{A}=\frac{1}{2}sđ\overset\frown{BCD}$ nên tính được góc C và A. + Trừ vế với vế của (1) cho (2), ta có \(\widehat {DOA} + \widehat {COD} - \widehat {AOB} - \widehat {BOC} = {40^o}\) hay \(sđ\overset\frown{CDA}-sđ\overset\frown{ABC}={{40}^{o}}\), biết \(sđ\overset\frown{CDA}+sđ\overset\frown{ABC}={{360}^{o}}\). + $\widehat{B}=\frac{1}{2}sđ\overset\frown{CDA};\widehat{D}=\frac{1}{2}sđ\overset\frown{ABC}$ nên tính được góc B và góc D. Lời giải chi tiết Vì tổng các góc trong tam giác \(ADE\) bằng 180o nên \(\hat A + \hat D = {180^ \circ } - \widehat E = {140^ \circ }\). Do vậy \(\frac{1}{2}\left( {\widehat {BOC} + \widehat {COD}} \right) + \frac{1}{2}\left( {\widehat {AOB} + \widehat {BOC}} \right) = {140^o}\) Suy ra \(\frac{1}{2}\left( {{{360}^o} + \widehat {BOC} - \widehat {AOD}} \right) = {140^o}\), hay \(\widehat {DOA} - \widehat {BOC} = {80^o}\) (1) Mặt khác, tổng các góc trong tam giác ABF bằng 180o nên \(\hat A + \hat B = {180^ \circ } - \widehat F = {160^ \circ }\). Do vậy \(\frac{1}{2}\left( {\widehat {BOC} + \widehat {COD}} \right) + \frac{1}{2}\left( {\widehat {COD} + \widehat {DOA}} \right) = {160^o}\) Suy ra \(\frac{1}{2}\left( {{{360}^o} + \widehat {COD} - \widehat {AOB}} \right) = {160^o}\), hay \(\widehat {AOB} - \widehat {COD} = {40^o}\) (2) Cộng vế với vế của (1) và (2), ta được \(\widehat {AOB} + \widehat {DOA} - \widehat {COD} - \widehat {BOC} = {120^o}\) hay \(sđ\overset\frown{DAB}-sđ\overset\frown{BCD}={{120}^{o}}\), chú ý rằng \(sđ\overset\frown{DAB}+sđ\overset\frown{BCD}={{360}^{o}}\) Suy ra: $\widehat{C}=\frac{1}{2}sđ\overset\frown{DAB}=\frac{{{120}^{o}}+{{360}^{o}}}{4}={{120}^{o}}$; $\widehat{A}=\frac{1}{2}sđ\overset\frown{BCD}=\frac{{{360}^{o}}-{{120}^{o}}}{4}={{60}^{o}}$. Trừ vế với vế của (1) cho (2), ta được \(\widehat {DOA} + \widehat {COD} - \widehat {AOB} - \widehat {BOC} = {40^o}\) hay \(sđ\overset\frown{CDA}-sđ\overset\frown{ABC}={{40}^{o}}\), chú ý rằng \(sđ\overset\frown{CDA}+sđ\overset\frown{ABC}={{360}^{o}}\) Suy ra: $\widehat{B}=\frac{1}{2}sđ\overset\frown{CDA}=\frac{{{40}^{o}}+{{360}^{o}}}{4}={{100}^{o}}$; $\widehat{D}=\frac{1}{2}sđ\overset\frown{ABC}=\frac{{{360}^{o}}-{{40}^{o}}}{4}={{80}^{o}}$.
|