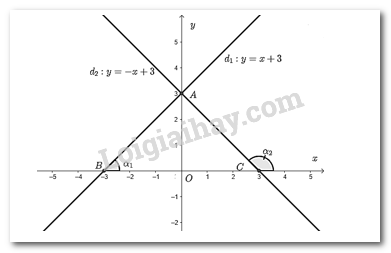
Giải Bài 19 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo

a)

a) Bằng cách vẽ hình, tìm tọa độ giao điểm \(A\) của hai đường thẳng nói trên và tìm các giao điểm \(B,C\) lần lượt của \({d_1}\) và \({d_2}\) với trục \(Ox\).

Phương pháp giải:

- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:

Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).

Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).

Lời giải chi tiết:

- Vẽ đồ thị hàm số \(y = x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} =  - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).

- Vẽ đồ thị hàm số \(y =  - x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y =  - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).

Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).

Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).

Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).

b)

b) Dùng thước đo góc để tìm góc tạo bởi \({d_1}\) và \({d_2}\) lần lượt với trục \(Ox\).

Phương pháp giải:

Đo góc

Lời giải chi tiết:

Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).

Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).

c)

c) Tính chu vi và diện tích của tam giác \(ABC\).

Phương pháp giải:

- Chu vi tam giác: \(C = a + b + c\) với \(a,b,c\) là ba cạnh tam giác.

- Diện tích tam giác: \(S = \dfrac{1}{2}a.{h_a}\) với \(a\) là độ dài đáy, \({h_a}\) là độ dài chiều cao tương ứng.

Lời giải chi tiết:

Vì \(Ox \bot Oy\) tại \(O\)nên tam giác \(AOB\) và tam giác \(AOC\) đều vuông tại \(O\).

Ta có: \(OA = 3;OB = 3;OC = 3\)

\(BC = OB + OC = 3 + 3 = 6\).

Áp dụng định lí Py – ta – go cho tam giác \(AOB\) ta có:

\(O{A^2} + O{B^2} = A{B^2}\)

\( \Leftrightarrow {3^2} + {3^2} = A{B^2}\)

\( \Leftrightarrow A{B^2} = 9 + 9 = 18\)

\( \Leftrightarrow AB = \sqrt {18}  = 3\sqrt 2 \)

Áp dụng định lí Py – ta – go cho tam giác \(AOC\) ta có:

\(O{A^2} + O{C^2} = A{C^2}\)

\( \Leftrightarrow {3^2} + {3^2} = A{C^2}\)

\( \Leftrightarrow A{C^2} = 9 + 9 = 18\)

\( \Leftrightarrow AC = \sqrt {18}  = 3\sqrt 2 \)

Chu vi tam giác \(ABC\) là:

\(C = AB + AC + BC = 3\sqrt 2  + 3\sqrt 2  + 6 = 6 + 6\sqrt 2 \) (đơn vị độ dài)

Vì \(Ox \bot Oy\) nên \(OA\) vuông góc với \(BC\) tại \(O\). Do đó, \(OA\) là đường cao  tam giác \(ABC\) ứng với cạnh \(BC\).

Diện tích tam giác \(ABC\) là:

\(S = \dfrac{1}{2}OA.BC = \dfrac{1}{2}.3.6 = 9\) (đơn vị diện tích)

Vậy chu vi tam giác \(ABC\) là \(6 + 6\sqrt 2 \) đơn vị độ dài và diện tích tam giác \(ABC\) là 9 đơn vị diện tích.