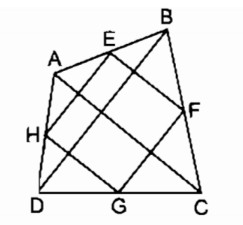
Bài 157 trang 99 SBT Toán 8 tập 1

Đề bài

Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là:

a. Hình chữ nhật

b. Hình thoi

c. Hình vuông

Lời giải chi tiết

Trong ∆ ABC ta có EF là đường trung bình nên EF // AC và EF = $\displaystyle {1 \over 2}$AC (1)

Trong ∆ ADC ta có HG là đường trung bình nên HG // AC và HG = $\displaystyle {1 \over 2}$AC (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Vậy tứ giác EFGH là hình bình hành

a. Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF

Mà $EF//AC$ (chứng minh trên) và $EH//BD;EH=\dfrac{1}2BD$ (do EH là đường trung bình của tam giác ABD)

Do đó $EH ⊥ EF⇔ AC ⊥ BD$

Vậy tứ giác EFGH là hình chữ nhật thì $AC ⊥ BD$

b. Hình bình hành EFGH là hình thoi ⇔ EH = EF

Mà EF = $\displaystyle {1 \over 2}$AC (chứng minh trên) và $EH=\dfrac{1}2BD$ (chứng minh trên)

Nên $EH = EF⇔ AC = BD$ 

Vậy tứ giác EFGH là hình thoi thì $AC = BD$

c. Tứ giác EFGH là hình vuông khi EFGH vừa là hình thoi, vừa là hình chữ nhật.

Từ câu a, b suy ra tứ giác EFGH là hình vuông $⇔ AC ⊥ BD$ và $AC = BD$

HocTot.Nam.Name.Vn