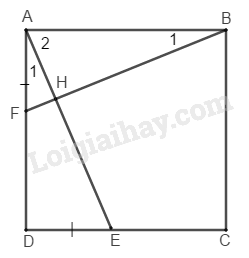
Bài 149 trang 98 SBT Toán 8 tập 1Giải bài 149 trang 98 sách bài tập toán 8. Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF... Đề bài Cho hình vuông \(ABCD.\) Trên cạnh \(AD\) lấy điểm \(F,\) trên cạnh \(DC\) lấy điểm \(E\) sao cho \(AF = DE.\) Chứng minh rằng \(AE = BF\) và \(AE ⊥ BF.\) Phương pháp giải - Xem chi tiết - Vận dụng kiến thức về các trường hợp bằng nhau của tam giác. - Áp dụng định lí: Tổng ba góc trong một tam giác bằng \(180^0\) Lời giải chi tiết
Xét \(∆ ABF\) và \(∆ DAE:\) \(AB = DA\) (gt) \(\widehat {BAF} = \widehat {ADE} = {90^0}\) \(AF = DE\) (gt) Do đó: \(∆ ABF = ∆ DAE\, (c.g.c)\) \(⇒ BF = AE\) và \({\widehat B_1} = {\widehat A_1}\) Gọi \(H\) là giao điểm của \(AE\) và \(BF.\) \(\widehat {BAF} = {\widehat A_1} + {\widehat A_2} = {90^0}\) Suy ra: \({\widehat B_1} + {\widehat A_2} = {90^0}\) Trong \(∆ ABH\) ta có: \(\widehat {AHB} + {\widehat B_1} + {\widehat A_2} = {180^0}\) \(\widehat {AHB} = {180^0} - \left( {{{\widehat B}_1} + {{\widehat A}_2}} \right)\)\( = {180^0} - {90^0} = {90^0}\) Vậy \(AE ⊥ BF\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
