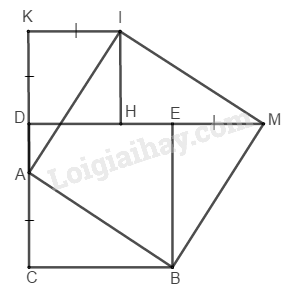
Bài 152 trang 99 SBT Toán 8 tập 1

Đề bài

Cho hình vuông \(DEBC.\) Trên cạnh \(CD\) lấy điểm \(A,\) trên tia đối của tia \(DC\) lấy điểm \(K,\) trên tia đối tia \(ED\) lấy điểm \(M\) sao cho \(CA = DK = EM.\) Vẽ hình vuông \(DKIH\) (\(H\) thuộc cạnh \(DE\)). Chứng minh rằng \(ABMI\) là hình vuông.

Lời giải chi tiết

Xét \(∆ CAB\) và \(∆ EMB :\)

\(CA = ME\) (gt)

\(\widehat {ACB} = \widehat {BEM} = {90^0}\)

\(CB = EB\) (tính chất hình vuông)

Do đó: \(∆ CAB = ∆ EMB\, (c.g.c)\)

\(⇒ AB = MB\) (1)

\(AK = DK +DA\)

\(CD = CA + AD\)

mà \(CA = DK\) nên \(AK = CD\)

Xét \(∆ CAB\) và \(∆ KIA :\)

\(CA = KI\) (vì cùng bằng \(DK\))

\(\widehat C = \widehat K = {90^0}\)

\(CB = AK\) (vì cùng bằng \(CD\))

Do đó: \(∆ CAB = ∆ KIA\, (c.g.c)\)

\(⇒ AB = AI\) (2)

Ta có: \(DH = DK\) (vì \(KDHI\) là hình vuông)

\(EM = DK\) (gt)

\(⇒ DH + HE = HE + EM\)

hay \( DE = HM\)

Xét \(∆ HIM\) và \(∆ EMB :\)

\(HI = EM\) (vì cùng bằng \(DK\))

\(\widehat H = \widehat E = {90^0}\)

\(HM = EB\) (vì cùng bằng \(DE\))

Do đó: \(∆ HIM = ∆ EMB\, (c.g.c)\)

\(⇒ IM = MB\) (3)

Từ (1), (2) và (3) suy ra: \(AB = BM = AI = IM\)

Tứ giác \(ABMI\) là hình thoi.

Mặt khác, ta có \(∆ ACB = ∆ MEB\) (chứng minh trên)

\(\eqalign{  &  \Rightarrow \widehat {CBA} = \widehat {EBM}  \cr  & \widehat {CBA} + \widehat {ABE} = \widehat {CBE} = {90^0} \cr} \)

Suy ra: \(\widehat {EBM} + \widehat {ABE} = {90^0}\) hay \(\widehat {ABM} = {90^0}\)

Vậy : Tứ giác \(ABMI\) là hình vuông.

HocTot.Nam.Name.Vn