Giải bài 1.40 trang 27 sách bài tập toán 12 - Kết nối tri thứcMột khối bưu kiện có hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là (240) cm. Gọi (x) là độ dài cạnh của thiết diện ngang. a) Tính thể tích của khối bưu kiện theo (x). b) Kí hiệu (Vleft( x right)) là thể tích của khối bưu kiện. Khảo sát sự biến thiên của hàm số (y = Vleft( x right)). Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Một khối bưu kiện có hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là \(240\) cm. Gọi \(x\) là độ dài cạnh của thiết diện ngang. a) Tính thể tích của khối bưu kiện theo \(x\). b) Kí hiệu \(V\left( x \right)\) là thể tích của khối bưu kiện. Khảo sát sự biến thiên của hàm số \(y = V\left( x \right)\).
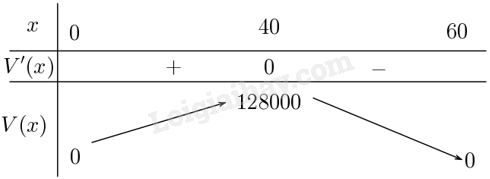
Phương pháp giải - Xem chi tiết Ý a: + Gọi chiều dài là y, biểu diễn \(y\) theo \(x\). + Xác định công thức thể tích \(V\left( x \right) = x \cdot y \cdot x\). Ý b: Khảo sát hàm số \(V\left( x \right)\). Lời giải chi tiết a) Giả sử chiều dài là \(y\), ta có \(y + 4x = 240\) suy ra \(y = - 4x + 240\). Khi đó thể tích khối bưu kiện là \(x \cdot y \cdot x = x \cdot \left( { - 4x + 240} \right) \cdot x = {x^2} \cdot \left( { - 4x + 240} \right)\) (cm3) b) Xét hàm số \(V\left( x \right) = {x^2} \cdot \left( { - 4x + 240} \right)\). Tập xác định: \(\left( {0;60} \right)\). Sự biến thiên: \(V'\left( x \right) = 480x - 12{x^2}\) khi đó \(V'\left( x \right) = 0 \Leftrightarrow 480x - 12{x^2} = 0 \Leftrightarrow x = 40\) do \(x > 0\). + Hàm số đồng biến trên khoảng \(\left( {0;40} \right)\), nghịch biến trên \(\left( {40;60} \right)\). + Hàm số đạt cực đại tại \(x = 40\) với \({{V}_{C}}=128000\)cm3. + Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } N\left( t \right) = 1200\) + Bảng biến thiên:
|