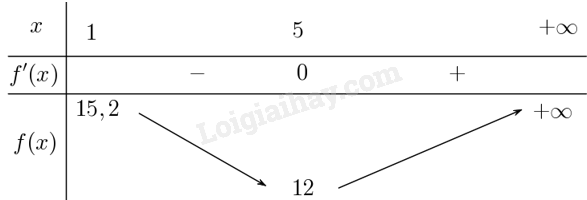
Giải bài 1.37 trang 26 sách bài tập toán 12 - Kết nối tri thứcGiả sử chi phí để sản xuất (x) sản phẩm của một nhà máy được cho bởi (Cleft( x right) = 0,2{x^2} + 10x + 5) (triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là (fleft( x right) = frac{{Cleft( x right)}}{x}). a) Khảo sát sự biến thiên của hàm số (y = fleft( x right)). b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất? Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Giả sử chi phí để sản xuất \(x\) sản phẩm của một nhà máy được cho bởi \(C\left( x \right) = 0,2{x^2} + 10x + 5\) (triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\). a) Khảo sát sự biến thiên của hàm số \(y = f\left( x \right)\). b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất? Phương pháp giải - Xem chi tiết Ý a: Khảo sát hàm số \(y = f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{0,2{x^2} + 10x + 5}}{x}\) theo các bước đã học. Ý b: Từ bảng biến thiên suy ra giá trị nhỏ nhất của hàm số. Lời giải chi tiết a) Xét hàm số \(y = f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{0,2{x^2} + 10x + 5}}{x}\) . Tập xác định \(\left[ {1; + \infty } \right)\). Sự biến thiên: \(f'\left( x \right) = {\left( {\frac{{0,2{x^2} + 10x + 5}}{x}} \right)^\prime } = \frac{{0,2{x^2} - 5}}{{{x^2}}}\). Khi đó \(f'\left( x \right) = 0 \Leftrightarrow \frac{{0,2{x^2} - 5}}{{{x^2}}} = 0 \Leftrightarrow x = 5\) do \(x \ge 1\). + Ta có \(S'\left( x \right) = 0 \Leftrightarrow \frac{{6{{\left( {x - 4} \right)}^2} - 1200}}{{{{\left( {x - 4} \right)}^2}}} = 0 \Leftrightarrow 6{\left( {x - 4} \right)^2} - 1200 = 0 \Leftrightarrow x = 4 + 10\sqrt 2 \). + Hàm số đồng biến trên khoảng \(\left( {5; + \infty } \right)\), nghịch biến trên khoảng \(\left( {1;5} \right)\). + Hàm số đạt cực tiểu tại \(x = 5\) với \({f_{CT}} = 12\). + Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) + Bảng biến thiên:
b) Từ bảng biến thiên suy ra số lượng sản phẩm cần sản xuất là \(x = 5\) để chi phí sản xuất trung bình là thấp nhất: \({f_{CT}} = 12\).
|