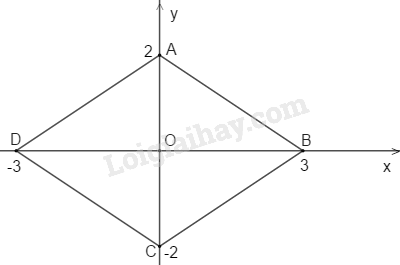
Bài 135 trang 97 SBT Toán 8 tập 1

Đề bài

Tứ giác $ABCD$ có tọa độ các đỉnh như sau: $A(0; 2),$ $B( 3; 0),$ $C(0; −2 ),$ $D(−3; 0).$ Tứ giác $ABCD$ là hình gì? Tính chu vi của tứ giác đó?

Lời giải chi tiết

Vì $A(0; 2)$ và $C(0; −2)$ nên hai điểm $A$ và $C$ đối xứng nhau qua $O (0, 0)$ $⇒ OA = OC$

Vì $B(3; 0)$ và $D(−3; 0)$ nên hai điểm $B$ và $D$ đối xứng qua $O (0; 0)$ $⇒ OB = OD$

Tứ giác $ABCD$ là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

$Ox ⊥ Oy$ hay $AC ⊥ BD$

Vậy tứ giác $ABCD$ là hình thoi

Trong $∆ OAB$ vuông tại $O.$ Theo định lý Pi-ta-go ta có:

$\eqalign{  & A{B^2} = O{A^2} + O{B^2}  \cr  & A{B^2} = {2^2} + {3^2} = 4 + 9 = 13  \cr & AB = \sqrt {13}  \cr}$

Chu vi hình thoi bằng $4\sqrt {13}$

HocTot.Nam.Name.Vn