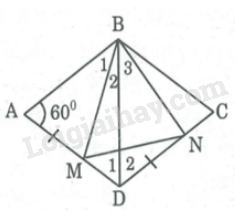
Bài 140 trang 97 SBT Toán 8 tập 1

Đề bài

Hình thoi \(ABCD\) có \(\widehat A = {60^0}\) . Trên cạnh \(AD\) lấy điểm \(M,\) trên cạnh \(DC\) lấy điểm \(N\) sao cho \(AM = DN.\) Tam giác \(BMN\) là tam giác gì ? Vì sao ?

Lời giải chi tiết

Nối \(BD,\) ta có:

\(AB = AD=BC=BD\) (do ABCD là hình thoi) nên \(∆ ABD\) cân tại \(A\) 

Mà  \(\widehat A = {60^0}\)

Nên \(∆ ABD\) đều.

\( \Rightarrow \widehat {ABD} = {\widehat D_1} = {60^0}\)  và \(BD = AB\)

Suy ra: \(BD = BC = CD\)

Vậy \(∆ CBD\) đều.

\( \Rightarrow {\widehat D_2} = {60^0}\)

Xét \(∆ BAM\) và \(∆ BDN:\)

\(AB = BD\) (chứng minh trên)

\(\widehat A = {\widehat D_2} = {60^0}\)

\(AM = DN\) (giả thiết)

Do đó: \(∆ BAM = ∆ BDN \,(c.g.c)\) \( \Rightarrow {\widehat B_1} = {\widehat B_3}\)  và \(BM = BN\)

Suy ra: \(∆ BMN\) cân tại \(B\)

\({\widehat B_2} + {\widehat B_1} = \widehat {ABD} = {60^0}\)

Suy ra: \({\widehat B_2} + {\widehat B_3} = \widehat {MBN} = {60^0}\)

Vậy \(∆ BMN\) đều (tam giác cân có 1 góc bằng \(60^0\) là tam giác đều)

HocTot.Nam.Name.Vn