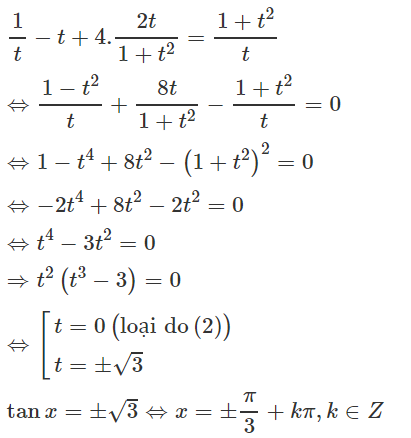Bài 1.31 trang 38 SBT đại số và giải tích 11Giải bài 1.31 trang 38 sách bài tập đại số và giải tích 11. Tìm tập xác định của các hàm số... Đề bài Giải phương trình \(\cot x-\tan x+4\sin 2x=\dfrac{2}{\sin 2x}\) Phương pháp giải - Xem chi tiết Tìm ĐKXĐ của phương trình. Sử dụng công thức \(\tan x=\dfrac{\sin x}{\cos x}\) và \(\cot x=\dfrac{\cos x}{\sin x}\) để biến đổi phương trình. Sử dụng công thức nhân đôi. Sử dụng công thức \({\sin}^2 x+{\cos}^2 x=1\). Lời giải chi tiết ĐKXĐ: \(\sin x\ne 0\) và \(\cos x\ne 0\) \(\Leftrightarrow \sin 2x\ne 0\) \(\Leftrightarrow \cos 2x\ne \pm 1\) Ta có: \(\cot x-\tan x+4\sin 2x=\dfrac{2}{\sin 2x}\) \(\Leftrightarrow \dfrac{\cos x}{\sin x}-\dfrac{\sin x}{\cos x}+4\sin 2x=\dfrac{2}{\sin 2x} \) \(\Leftrightarrow \dfrac{{\cos}^2 x-{\sin}^2 x}{\sin x\cos x}+4\sin 2x=\dfrac{2}{\sin 2x} \) \(\Leftrightarrow \dfrac{\cos 2x}{\dfrac{\sin 2x}{2}}+4\sin 2x=\dfrac{2}{\sin 2x} \) \(\Leftrightarrow \dfrac{2\cos 2x}{\sin 2x}+4\sin 2x=\dfrac{2}{\sin 2x} \) \(\Leftrightarrow 2\cos 2x+4{\sin}^2 2x=2\) \(\Leftrightarrow 2\cos 2x+4(1-{\cos}^2 2x)=2\) \(\Leftrightarrow 4{\cos}^2 2x-2\cos 2x+2=0\) \(\Leftrightarrow \left[ \begin{array}{l} \cos 2x=1\text{(loại)}\\\cos 2x=-\dfrac{1}{2}\end{array} \right. \) \(\Leftrightarrow 2x=\pm\dfrac{2\pi}{3}+k2\pi,k\in\mathbb{Z}\) \(\Leftrightarrow x=\pm\dfrac{\pi}{3}+k\pi,k\in\mathbb{Z}\). Cách khác: Đặt t = tanx Điều kiện t ≠ 0 Phương trình đã cho có dạng
HocTot.Nam.Name.Vn
|