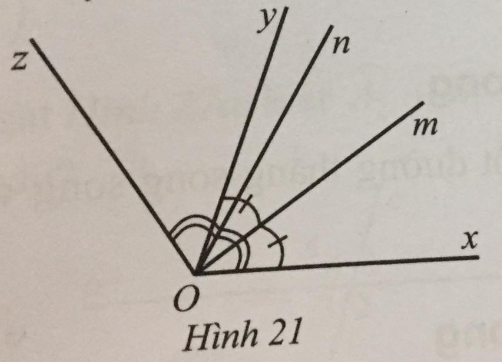
Giải Bài 13 trang 107 sách bài tập toán 7 tập 1 - Cánh diềuỞ Hình 21 có Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Ở Hình 21 có ^xOy=70∘,^xOz=120∘, hai tia Om và On lần lượt là tia phân giác của góc xOy và xOz. Tính số đo mỗi góc yOz, xOm, xOn, mOn.
Phương pháp giải - Xem chi tiết Tính số mỗi góc dựa vào Om, On lần lượt là phân giác của các góc xOy và xOz. Lời giải chi tiết Ta có: Om và On lần lượt là tia phân giác của góc xOy và xOz nên ^xOm=^yOm=70∘:2=35∘^xOn=^zOn=120∘:2=60∘ Suy ra ^yOz=^zOn−^yOn=^zOn−(^xOy−^xOn)⇒^yOz=60∘−(70∘−60∘)=50∘ ^mOn=^xOy−^yOn−^xOm=70∘−10∘−35∘=25∘. Vậy ^yOz=50∘,^xOm=35∘,^xOn=60∘,^mOn=25∘.
|