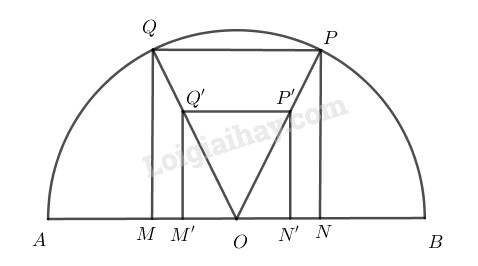
Bài 1.25 trang 33 SBT hình học 11

Đề bài

Cho nửa đường tròn đường kính $AB$. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính $AB$ của nửa đường tròn đó.

Lời giải chi tiết

Gọi $O$ là trung điểm của$AB$. Giả sử dựng được hình vuông $MNPQ$ có $M$, $N$ thuộc đường kính $AB$, $P$, $Q$ thuộc nửa đường tròn. Khi đó $O$ phải là trung điểm của $MN$.  Nếu lấy một hình vuông $M’N’P’Q’$ sao cho $M’$, $N’$ thuộc $AB$, $O$ là trung điểm của $M’N’$ khi đó ta thấy $\dfrac{OM}{OM’}=\dfrac{ON}{ON’}=\dfrac{OP}{OP’}=\dfrac{OQ}{OQ’}$

Từ đó suy ra hình vuông $MNPQ$ là ảnh của hình vuông $M’N’P’Q’$ qua phép vị tự tâm $O$, suy ra $O$, $P$, $P’$ và $O$, $Q$, $Q’$ thẳng hàng.

Vậy ta có cách dựng:

- Dựng hình vuông $M’N’P’Q’$ nằm trong nửa hình tròn đã cho sao cho $M’N’$ thuộc $AB$ và $O$ là trung điểm của $M’N’$. Tia $OP’$ cắt nửa đường tròn tại $P$; tia $OQ’$ cắt nửa đường tròn tại $Q$ .

Khi đó dễ thấy tứ giác $MNPQ$ là hình vuông cần dựng.

HocTot.Nam.Name.Vn