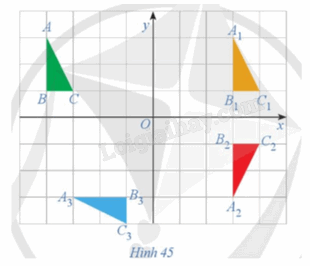
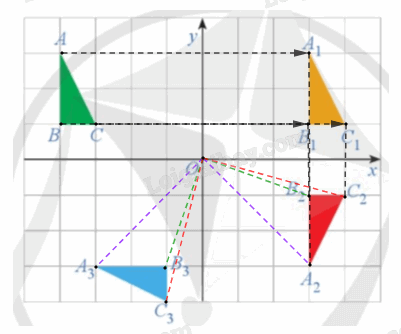
Giải bài 12 trang 25 Chuyên đề học tập Toán 11 Cánh diềuQuan sát Hình 45. Xác định các phép dời hình biến tam giác ABC thành tam giác A1B1C1, tam giác A1B1C1 thành tam giác A2B2C2, tam giác A2B2C2 thành tam giác A3B3C3. Đề bài Quan sát Hình 45. Xác định các phép dời hình biến tam giác ABC thành tam giác A1B1C1, tam giác A1B1C1 thành tam giác A2B2C2, tam giác A2B2C2 thành tam giác A3B3C3.
Phương pháp giải - Xem chi tiết Quan sát hình vẽ và dựa và các phép biến hình đã học để suy luận Lời giải chi tiết
+) Ta có: \(\overrightarrow {A{A_1}} = \overrightarrow {B{B_1}} = \overrightarrow {C{C_1}} \) nên ta có phép tịnh tiến theo vectơ \(\overrightarrow {A{A_1}} \) biến các điểm A, B, C tương ứng thành các điểm A1, B1, C1. Do đó, phép tịnh tiến theo vectơ \(\overrightarrow {A{A_1}} \) biến tam giác ABC thành tam giác \({A_1}{B_1}{C_1}.\) +) Ox là đường trung trực của các đoạn thẳng A1A2, B1B2 và C1C2 nên ta có phép đối xứng trục Ox biến các điểm A1, B1, C1 tương ứng thành các điểm A2, B2, C2. Do đó, phép đối xứng trục Ox biến tam giác A1B1C1 thành tam giác \({A_2}{B_2}{C_2}.\) +) Ta có: \(\;O{A_2}\; = {\rm{ }}O{A_3},{\rm{ }}O{B_2}\; = {\rm{ }}O{B_3},{\rm{ }}O{C_2}\; = {\rm{ }}O{C_3}\;\) (đường chéo của các hình chữ nhật có cùng kích thước) và \(\widehat {{A_2}O{A_3}} = \widehat {{B_2}O{B_3}} = \widehat {{C_2}O{C_3}} = 90^\circ \), phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ, do đó phép quay tâm O với góc quay – 90° biến các điểm A2, B2, C2 tương ứng thành các điểm A3, B3, C3. Vậy ta có phép quay tâm O với góc quay – 90° biến tam giác A2B2C2 thành tam giác A3B3C3.
|