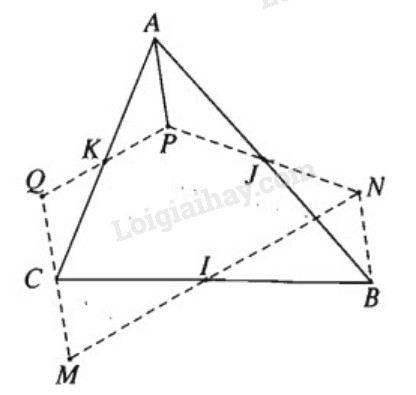
Bài 1.14 trang 21 SBT hình học 11

Đề bài

Cho ba điểm không thẳng hàng $I$, $J$, $K$. Hãy dựng tam giác $ABC$ nhận $I$, $J$, $K$ lần lượt là trung điểm của các cạnh $BC$, $AB$, $AC$.

Lời giải chi tiết

Giả sử tam giác $ABC$ đã dựng được.

Cách dựng điểm $C$:

Lấy điểm $M$ bất kì. Gọi $N$ là ảnh của $M$ qua phép đối xứng tâm $I$. $P$ là ảnh của $N$ qua phép đối xứng tâm $J$. $Q$ là ảnh của $P$ qua phép đối xứng tâm $K$.

Khi đó $\vec{CM}=-\vec{BN}=\vec{AP}=-\vec{CQ}$.

Do đó $C$ là trung điểm của $QM$.

Tương tự, cách dựng điểm $B$:

Lấy điểm $O$ bất kỳ, gọi $O_1$ là ảnh của $O$ qua phép đối xứng tâm $J$, $O_2$ là ảnh của $O_1$ qua phép đối xứng tâm $K$, $O_3$ là ảnh của $O_2$ qua phép đối xứng tâm $I$

$B$ là trung điểm của $OO_3$.

Cách dựng điểm $A$:

Lấy điểm $H$ bất kỳ, gọi $H_1$ là ảnh của $H$ qua phép đối xứng tâm $J$, $H_2$ là ảnh của $H_1$ qua phép đối xứng tâm $K$, $H_3$ là ảnh của $H_2$ qua phép đối xứng tâm $I$

$A$ là trung điểm của $HH_3$.

Từ đó suy ra cách dựng tam giác $ABC$.

 HocTot.Nam.Name.Vn