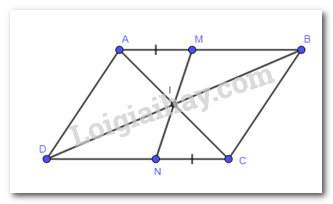
Giải bài 11 trang 121 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Cho bình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:

a) $\Delta IAM = \Delta ICN$

b) Tứ giác AMCN là hình bình hành.

c) Ba điểm B, I, D thẳng hàng.

Lời giải chi tiết

a) Xét tam giác IAM ta có: $\widehat {AMI} + \widehat {MIA} + \widehat {MAI} = {180^o}$

Xét tam giác ICN có: $\widehat {CNI} + \widehat {NIC} + \widehat {NCI} = {180^o}$

Vì: $\widehat {MIA} = \widehat {NIC}$ (đối đỉnh)

$\widehat {MAI} = \widehat {NCI}$ (do AB // CD)

Suy ra: $\widehat {AMI} = \widehat {CNI}$

Xét tam giác IAM  và tam giác ICN có:

$\widehat {AMI} = \widehat {CNI}$

AM = CN

$\widehat {MIA} = \widehat {NIC}$

Suy ra $\Delta IAM = \Delta ICN(g - c - g)$

b) Ta có: AM = CN (gt)

AM // CN (vì M $\in$ AB, N $\in$ CD)

Suy ra tứ giác AMCN là hình bình hành.

c) Vì tứ giác AMCN là hình bình hành

Suy ra I là trung điểm của AC

Suy ra I là trung điểm của BD (vì ABCD là hình bình hành)

Suy ra ba điểm B, I, D thẳng hàng.