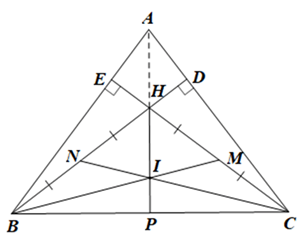
Giải Bài 105 trang 99 sách bài tập toán 7 - Cánh diềuCho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H. a) Chứng minh ∆ADB = ∆AEC. b) Chứng minh tam giác HDE là tam giác cân. c) So sánh HB và HD. d) Gọi M là trung điểm của HC, N là trung điểm của HB, I là giao điểm của BM và CN. Chứng minh ba điểm A, H, I thẳng hàng. Phương pháp giải - Xem chi tiết - Chứng minh: ∆ADB = ∆AEC (cạnh huyền – góc nhọn). - Chứng minh: HE = HD nên tam giác HDE cân tại H. - Chứng minh: HC > HD và HB = HC nên HB > HD. - Chứng minh: HP ⊥ BC hay HI ⊥ BC và AH ⊥ BC suy ra ba điểm A, H, I cùng nằm trên một đường thẳng vuông góc với BC tại P Lời giải chi tiết a) Xét ∆ABD và ∆ACE có: \(\widehat {ADB} = \widehat {AEC}\left( { = 90^\circ } \right)\) AB = AC (do tam giác ABC cân tại A), \(\hat A\) là góc chung, Suy ra ∆ADB = ∆AEC (cạnh huyền – góc nhọn). Vậy ∆ADB = ∆AEC. b) Vì ∆ADB = ∆AEC (chứng minh câu a) Suy ra AD = AE (hai cạnh tương ứng) và \(\widehat {ABD} = \widehat {ACE}\) (hai góc tương ứng). Ta có AB = AE + EB, AC = AD + DC. Mà AB = AC, AE = AD. Suy ra BE = CD. Xét ∆EHB và ∆DHC có: \(\widehat {HEB} = \widehat {H{\rm{D}}C}\left( { = 90^\circ } \right)\) BE = CD (chứng minh trên), \(\widehat {EBH} = \widehat {DCH}\) (do \(\widehat {ABD} = \widehat {ACE}\)) Suy ra ∆EHB = ∆DHC (cạnh góc vuông – góc nhọn kề). Do đó HE = HD, BH = CH (các cặp cạnh tương ứng). Tam giác HDE có HE = HD nên tam giác HDE cân tại H. Vậy tam giác HDE là tam giác cân tại H. c) Trong tam giác vuông HDC có HC > HD (trong tam giác vuông, cạnh huyền là cạnh lớn nhất) Mà HC = HB (chứng minh câu b) Do đó HB > HD. Vậy HB > HD. d) • Gọi P là giao điểm của HI và BC. Tam giác HBC có BM và CN là hai đường trung tuyến cắt nhau tại I. Do đó I là trọng tâm của tam giác HBC nên HP là đường trung tuyến xuất phát từ đỉnh H của tam giác. Từ đó ta có PB = PC. Xét ∆HBP và ∆HCP có: HB = HC (chứng minh ở câu b), HP là cạnh chung, PB = PC (chứng minh trên) Do đó ∆HBP = ∆HCP (c.c.c) Suy ra \(\widehat {HPB} = \widehat {HPC}\) (hai góc tương ứng) Mà \(\widehat {HPB} + \widehat {HPC} = 180^\circ \) (hai góc kề bù) Do đó \(\widehat {HPB} = \widehat {HPC} = \frac{{180^\circ }}{2} = 90^\circ \) Từ đó ta có HP ⊥ BC hay HI ⊥ BC (1) • Tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm của tam giác ABC. Do đó AH ⊥ BC (2) Từ (1) và (2) suy ra ba điểm A, H, I cùng nằm trên một đường thẳng vuông góc với BC tại P Hay ba điểm A, H, I thẳng hàng. Vậy ba điểm A, H, I thẳng hàng.
|