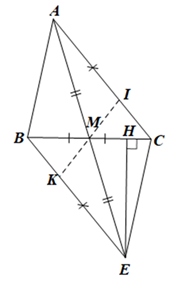
Giải Bài 104 trang 99 sách bài tập toán 7 - Cánh diềuCho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. a) Chứng minh AC = EB và AC song song với EB. b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh ba điểm I, M, K thẳng hàng. c) Từ E kẻ EH vuông góc với BC tại H. Cho biết \(\widehat {HBE} = 50^\circ ;\widehat {MEB} = 25^\circ \). Tính số đo các góc HEB và HEM. Phương pháp giải - Xem chi tiết - Chứng minh: ∆AMC = ∆EMB (c.g.c) suy ra AC = EB và chứng minh\(\widehat {MAC} = \widehat {MEB}\) suy ra AC song song với EB. - Chứng minh: \(\widehat {IMK} = 180^\circ \) suy ra ba điểm I, M, K tthẳng hàng. - Dựa vào tổng số đo hai góc gọn trong tam giác vuông bằng \({90^o}\) để tính số đo các góc HEB và HEM. Lời giải chi tiết a) Xét ∆AMC và ∆EMB có: AM = ME (giả thiết), \(\widehat {AMC} = \widehat {EMB}\) (hai góc đối đỉnh), BM = CM (vì M là trung điểm của BC) Do đó ∆AMC = ∆EMB (c.g.c) Suy ra AC = EB (hai cạnh tương ứng) và \(\widehat {MAC} = \widehat {MEB}\) (hai góc tương ứng) Mà \(\widehat {MAC}\) và \(\widehat {MEB}\) ở vị trí so le trong nên AC // BE. Vậy AC = EB và AC song song với EB. b) Xét ∆AMI và ∆EMK có: AM = ME (giả thiết), \(\widehat {MAI} = \widehat {MEK}\) (do \(\widehat {MAC} = \widehat {MEB}\)), AI = EK (giả thiết) Do đó ∆AMI = ∆EMK (c.g.c) Suy ra \(\widehat {AMI} = \widehat {EMK}\) (hai góc tương ứng) Mà \(\widehat {AMI} + \widehat {IME} = 180^\circ \) (hai góc kề bù) Suy ra \(\widehat {EMK} + \widehat {IME} = 180^\circ \) Hay \(\widehat {IMK} = 180^\circ \) Do đó ba điểm I, M, K thẳng hàng. Vậy ba điểm I, M, K thẳng hàng. c) Trong tam giác HBE vuông tại H có: \(\widehat {HBE} + \widehat {HEB} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°) Suy ra \(\widehat {HEB} = 90^\circ - \widehat {HBE} = 90^\circ - 50^\circ = 40^\circ \). Ta có \(\widehat {HEB} = \widehat {HEM} + \widehat {MEB}\) (hai góc kề nhau) Hay \(40^\circ = \widehat {HEM} + 25^\circ \) Suy ra \(\widehat {HEM} = 40^\circ - 25^\circ = 15^\circ \). Vậy \(\widehat {HEB} = 40^\circ ;\widehat {HEM} = 15^\circ \)
|