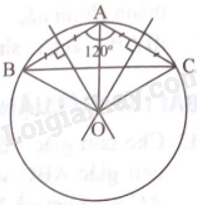
Giải bài 1 trang 79 sách bài tập toán 9 - Chân trời sáng tạo tập 2Cho tam giác ABC có AB = AC = 12 cm và (widehat {BAC} = {120^o}). Xác định tâm và tính bán kính của đường tròn (O; R) ngoại tiếp tam giác ABC. Đề bài Cho tam giác ABC có AB = AC = 12 cm và \(\widehat {BAC} = {120^o}\). Xác định tâm và tính bán kính của đường tròn (O; R) ngoại tiếp tam giác ABC. Phương pháp giải - Xem chi tiết Đường tròn ngoại tiếp tam giác có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kì của tam giác. Lời giải chi tiết
Vẽ đường trung trực của đoạn thẳng AB và AC cắt nhau tại điểm O. Ta có R = OA = OB = OC, suy ra đường tròn (O; R) ngoại tiếp tam giác ABC. Vì tam giác ABC cân tại A nên OA cũng là tia phân giác của \(\widehat A\), suy ra \(\widehat {OAB} = {60^o}\). Do đó tam giác OAB là tam giác đều. Vậy R = OA = AB = 12 (cm).  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
